Kumpulan Contoh Soal dan Pembahasan Soal Latihan Tegangan Regangan Modulus Elastisitas Young serta Rumusnya. Lengkap

|
| Kumpulan Contoh Soal dan Pembahasan Soal Latihan Tegangan Regangan Modulus Elastisitas Young serta Rumusnya. Lengkap |
Daftar Isi
- Deskripsi Singkat
- Rumus Modulus Young
- Kumpulan Contoh Soal dan Pembahasan Soal Latihan Tegangan Regangan Modulus Elastisitas Young
- Soal-soal latihan
Deskripsi Singkat
Modulus Young merupakan suatu ukuran untuk mengukur bagaimana
suaatu materi atau struktur rusak bila ditempatkan di bawah
tegangan.
Rumus Modulus Young
E = Modulus Young atau Modulus Elastisitas (N/m2)
Kumpulan Contoh Soal dan Pembahasan Soal Latihan Tegangan Regangan Modulus Elastisitas Young
1. Tentukan tegangan sebuah tali bila diketahui sebuah tali dengan diameter 20 mm dan ditarik dengan gaya 100 Newton.
Pembahasan
Diketahui :
Diameter tali (d) = 20 mm = 0,02 meter
Jari-jari tali (r) = 1 mm = 0,01 meter
Gaya tarik (F) = 100 Newton
Tegangan tali(σ)
Jawaban:
Luas penampang tali :
Tegangan tali :
Maka tegangan pada tali adalah 31,8 x 10^4 N/m2
2. Diketahui tegangan yang dialami suatu tali berdiameter 0,2 cm adalah 31,4 x 10^6 N/m^2. Tentukan besar gaya tarik yang dialaminya.
Pembahasan
Diketahui :
Diameter tali (d) = 0,2 cm = 0,002 meter
Jari-jari tali (r) = d/2 = 0,001 meter
Ditanya :
Gaya tarik (F)
Jawaban:
Luas penampang tali :
Tegangan tali :
Maka gaya tarik yang dialami tali adalah 98,596 Newton
3. Diketahui sebuah gaya tarik sebesar 100 Newton diberikan pada tali. Bila tegangan yang direncakana terjadi adalah 31,4 x 10^4 N/m^2. Tentukan Luas penampang tali tersebut.
Pembahasan
Diketahui :
Gaya tarik (F) = 100 Newton
Tegangan (σ) = 31,4 x 10^4 N/m^2
Ditanya : Luas penampang (A)
Jawaban:
Luas Penampang (A) :
Maka Luas penampang (A) tali adalah 3,18 x 10^(-6) m^2
4. Sebuah tali panjang nya 50 cm lalu ditarik sehingga panjangnya 0,8cm regangan tali tersebut adalah
Pembahasan
Diketahui : Panjang
awal tali (lo) = 50 cm
Pertambahan panjang (Δl)= 0,8 cm
Ditanya : Regangan tali
Jawaban:
Regangan tali :
Regangan (ε)=(Pertambahan panjang (Δl))/(Panjang awal (lo) )
Regangan (ε)=0,8/50
Regangan (ε)=0,016
Jadi regangan tali adalah 0,016
5. Seorang pemanjat tebing bergantung pada tali sepanjang 15 m Bila tali tersebut bertambah panjang 2.8 cm hitung regangan tali tersebut
Pembahasan
Diketahui :
Panjang awal tali (lo) = 15 m= 1500 cm
Pertambahan panjang (Δl)= 2,8 cm
Ditanya : Regangan tali
Jawaban:
Regangan tali :
Regangan (ε)=(Pertambahan panjang (Δl))/(Panjang awal (lo) )
Regangan (ε)=2.8/1500
Regangan (ε)=0.00187
Jadi regangan tali adalah 0.00187
6. Seutas tali mempunyai panjang mula mula 50 cm ditarik hingga tali tersebut mengalami pertambahan panjang 30 mm. Tentukan regangan tali!
Pembahasan
Diketahui : Panjang
awal tali (lo) = 50 cm
Pertambahan panjang (Δl)= 30 mm = 3cm
Ditanya : Regangan tali
Jawaban:
Regangan tali :
Regangan (ε)=(Pertambahan panjang (Δl))/(Panjang awal (lo) )
Regangan (ε)=3/50
Regangan (ε)=0,006
Jadi regangan tali adalah 0.006
7. Seutas tali mempunyai panjang mula-mula 100 cm. Tali mengalami regangan sebesar 0,002. Tentukan pertambahan Panjang serta panjang akhir dari tali tersebut.
Pembahasan
Diketahui : Panjang
awal tali (lo) = 100 cm
Regangan (ε)=0,002
Ditanya:
Pertambahan panjang (Δl)?
Panjang akhir (la)?
Jawaban:
Pertambahan Panjang tali :
Regangan (ε)=(Pertambahan panjang (Δl))/(Panjang awal (lo)
)
0,002=Δl/100
Δl=0,2 cm
Panjang tali akhir:
Panjang akhir(la)=Panjang awal (lo)+Pertambahan panjang (Δl)
Panjang akhir (la)=100+0,2=100,2 cm
Maka pertambahan panjang tali adalah 0,2 cm dan panjang akhir adalah 100,2 cm
8. Diketahui terdapat suatu tali ditarik dengan gaya 314 Newton sehingga panjang tali menjadi 1,02 meter. Bila panjang awal tali tersebut adalah 1 meter dan diameter tali tersebut adalah 10 mm. Tentukan:
a. Tegangan tali
b. Regangan tali
c. Modulus Elastisitas Young!
Pembahasan
Diketahui :
Gaya tarik (F) = 314 Newton
Panjang akhir tali (la ) = 1,02 meter
Panjang awal tali (lo) =
1 meter
Pertambahan panjang tali (Δl)= 1,02-1=0,02 meter
Diameter tali
(d) = 10 mm = 0,01 meter
Jari-jari tali (r) = 5 mm = 0,005 meter
Ditanya : (a) Tegangan (b) Regangan (c) Modulus Young
Jawaban:
(a) Tegangan
Luas penampang tali :
Mencari tegangan tali :
Maka tegangan pada tali adalah 4 x 10^6 N/m^2
(b) Regangan
9. Diketahui terdapat suatu tali senar ditarik dengan gaya 314 Newton. Bila panjang awal senar tersebut adalah 1 meter dan diameter senar tersebut adalah 10 mm. Tentukan pertambahan Panjang senar bila diketahui modulus youg tali adalah 2 x 10^8
Pembahasan
Diketahui :
Gaya tarik (F) = 314 Newton
Panjang awal tali (lo) = 1 meter
Diameter tali (d) = 10 mm =
0,01 meter
Jari-jari tali (r) = 5 mm = 0,005 meter
Modulus youg(E
)= 2 x 10^8
Ditanya : Pertambahan panjang tali (Δl) ?
Jawaban:
Maka Pertambahan panjang tali (Δl) 0,02 m
10. Tiang beton mempunyai tinggi 2 meter dan luas penampang lintang 1 m2 menopang beban bermassa 10.000 kg. Bila diketahui Modulus elastis Young Beton = 20 x 109 N/m2 dan gravitasi = 10 m/s2. Tentukan:
(a) tegangan tiang
(b) regangan tiang
(c) perubahan tinggi tiang!
Pembahasan
Diketahui :
Tinggi tiang (lo)= 2 meter
Luas penampang (A) = 1 m3
Massa
tiang (m)=10.000 kg
Modulus elastis Young Beton = 20 x 109 N/m2
Gravitasi
= 10 m/s2
Ditanya : (a) Tegangan tiang (b) Regangan tiang (c) Perubahan tinggi tiang!
Jawaban:
(a) Tegangan tiang
Gaya=berat= m.g= (10.000)(10)=105 Newton
Maka tegangan pada tiang adalah 10^5 N/m^2Maka regangan pada tiang adalah 5 x 10^(-6)
(c) Perubahan tinggi tiang
Maka perubahan tinggi tiang adalah 5 x 10^(-6)m atau tiang memendek sebesar 5 x 10^(-6) m
11. Sebuah tali panjangnya mula-mula 100 cm ditarik oleh gaya 10 N sehingga bertambah panjang sebesar 2 mm. Berapa regangan yang di alami tali
Pembahasan
Diketahui : Panjang
awal tali (lo) = 100 cm
Pertambahan panjang (Δl)= 2 mm = 0,2 cm
Gaya
tarik (F) = 10 N
Ditanya:
Regangan tali
Jawaban:
Regangan tali :
Regangan (ε)=(Pertambahan panjang (Δl))/(Panjang
awal (lo) )
Regangan (ε)=0,2/100
Regangan (ε)=0,002
Jadi regangan tali adalah 0,0002
12. Seutas tali mempunyai panjang mula-mula 150 cm ditarik hingga tali tersebut mengalami pertambahan panjang 2 mm. Tentukan regangan tali!
Pembahasan
Diketahui : Panjang
awal tali (lo) = 150 cm
Pertambahan panjang (Δl)= 2 mm=0,2 cm
Ditanya : Regangan tali
Jawab :
Regangan tali :
Regangan (ε)=(Pertambahan panjang (Δl))/(Panjang
awal (lo) )
Regangan (ε)=0,2/150
Regangan (ε)=0.0013
Jadi regangan tali adalah 0.0013
13. Dimensi dari modulus young adalah?
Jawab
Rumus Modulus young
Modulus Young (E)=
Tegangan(σ)/Regangan(ε) =(F/A)/(∆l/l)
Dimensi F -> MLT⁻²
Dimensi
A -> L²
Dimensi L -> L
Y = MLT⁻² / L² . L/L
Y = ML⁽¹⁻²⁾T⁻²
Y = ML⁻¹T⁻²
Y = M /
LT²
Dimensi = [M][L]^-1[T]^-2
14. Besar Modulus Young (Y) sebuah bahan (zat) dapat ditentukan dengan
menggunakan persamaan sebagai berikut:
Modulus Young (E)= Tegangan(σ)/Regangan(ε) =(F/A)/(∆l/l)
Pernyataan yang tepat tentang nilai modulus Young adalah
A. Semakin besar gaya (F) yang menarik bahan maka nilai Modulus Youngnya
makin besar.
B. Semakin besar luas penampang bahan (A) maka nilai
Modulus Youngnya makin besar.
C. Semakin besar panjang mula-mula
bahan (Lo) maka nilai modulus Youngnya makin kecil.
D. Semakin besar
luas penampang bahan (A) maka nilai Modulus Youngnya makin kecil
E.
Sebenarnya nilai Modulus Young bahan tidak bergantung pada gaya luar (F)
yang mempengaruhinya maupun ukuran geometri bahan
Jawaban:
Jawaban yang tepat adalah A. Semakin besar gaya (F) yang menarik bahan maka nilai Modulus Youngnya makin besar.
Penjelasan:
berdasarkan persamaan modulus young
E = F L/ ∆L. A
semakin kuat gaya F menarik bahan maka modulus young Y semakin besar
Soal Latihan
Tentukan:
3. Tentukan nilai modulus young sebuah tali. Bila diketahui nilai
tegangan dan regangan diambil dari soal 1 point a dan soal 2 point b
diatas.
Itu dia beberapa Kumpulan Contoh Soal dan Pembahasan Soal Latihan TeganganRegangan Modulus Elastisitas Young serta Rumusnya yang bisa dibagikan oleh masharist.com. Semoga bermanfaat.
Terinspirasi oleh :
gurumuda.net dan brainly :)

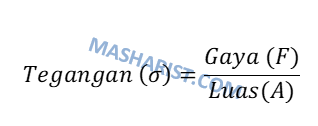




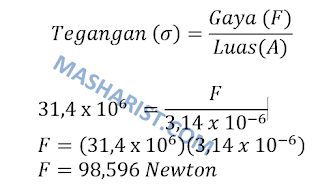




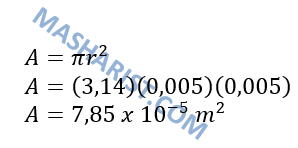








yg kumaksud bukan itu tapi perbandingan frekuensi satu dg yg lainnya
ReplyDelete