Kumpulan Contoh Soal dan Pembahasan Hukum Hooke dan Elastisitas serta Rumusnya. Lengkap
Assalammualaikum wr. wb. Apa kabar teman-teman? semoga semuanya pada
kesempatan kali ini masharist.com akan membagikan artikel tentang Contoh Soal Hukum Hooke dan Elastisitas. Contoh soal disini juga dilengkapi
dengan pembahasan. Contoh soal dan pembahasan berjumlah 51, dibagi berdasarkan tipe soal. Serta Soal latihan berjumlah 20. Semoga bermanfaat.
Daftar isi
- 1 Deskripsi Singkat Hukum Hooke
- 2 Contoh Soal Hukum Hooke dan Pembahasan
- 3 Hukum Hooke Energi Potensial Pegas
- 4 Elastis dan Plastis
- 5 Soal Latihan Hukum Hooke
1. Deskripsi Singkat Hukum Hooke
Bunyi Hukum Hooke :Bila pada sebuah pegas bekerja sebuah gaya, maka pegas tersebut akan bertambah panjang sebanding dengan besarnya gaya yang mempengaruhi pegas tersebut.
Rumus Hukum Hooke :
Besarnya pertambahan panjang benda :
· Sebanding dengan gaya penyebabnya dan
· Berbanding terbalik dengan konstannya
maka
Δx ~ F
Δx ~ 1/k
Δx = F/k atau F = k Δx
Batasan Hukum Hooke
Benda elastis memiliki batas elastisitas tertentu.
Jika benda elastis diberi gaya tertentu dan kemudian dilepaskan. Dapat terjadi 2 kemungkinan
1. Jika bentuk benda tidak kembali ke bentuk semula, berarti berarti gaya yang diberikan telah melewati batas elastisitasnya. Keadaan itu juga dinamakan keadaan plastis.
2. Jika bentuk benda kembali ke bentuk semula berarti gaya yang diberikan belum melewati batas elastisitasnya. Jika pegas kita lepaskan, pegas akan kembali ke posisi semula akibat gaya pemulih .
Ilustrasi Hukum Hooke dapat dilihat pada gambar dibawah:
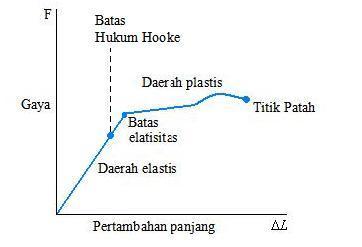 |
| Grafik Hubungan Gaya dan Pertambahan Panjang |
2. Contoh Soal Hukum Hooke dan Pembahasan
1.
Hukum hooke dinyatakan dengan persamaan F=-Kx. Tentukan dimensi dari
konstanta pegas.
a. MT^-2
b. MT^2
c. M^-2
d. T^-2
e.
M^-2 T^-2
Pembahasan
Diketahui :
F=-Kx
Ditanya : Dimensi
Konstanta (k)?
Jawaban :
F = - K.x
F = K. x ---> k = F/x
Dimensi F
F = m.a
= m. v/t
= m. s/t²
= M.L /T²
= MLT^-2
Dimensi
x : L
Dimensi k = MLT^-2 / L
= MT^-2
Maka dimensi dari Konstanta (k) adalah MT^-2 (a)
2.
(Soal UN 2000/2001 No. 1)
Diketahui sebuah batang serba sama (homogen) panjang L, ketika
ditarik dengan gaya F bertambah panjang sebesar ∆L. Agar pertambahan
panjang menjadi 4 ∆L maka besar gaya tariknya adalah …
A. 1/4 F
B.
1/2 F
C. 2 F
D. 4 F
E. 16 F
Pembahasan
Diketahui
:
Gaya tarik 1 (F1) = F
Pertambahan panjang 1 (∆x1) = ∆L
Pertambahan
panjang 2 (∆x2) = 4 ∆L
Ditanya : Gaya tarik 2 (F2)?
Jawaban
:
Rumus hukum Hooke :
F = k Δx
k = F / Δx
Batang
yang digunakan sama sehingga konstanta elastisitas (k) sama.
k1
= k2
F1 / ∆x1 = F2 / ∆x2
F / ΔL = F2 / 4ΔL
F / 1 = F2 /
4
F = F2 / 4
F2 = 4F
Maka besar gaya tariknya adalah
4F (D)
3. Sebuah batang baja homogen panjang L, ketika ditarik
dengan gaya F bertambah panjang sebesar ∆L. Agar pertambahan panjang
menjadi setengah dari awal ∆L maka besar gaya tariknya yang dikeluarkan
adalah …
A. 1/4 F
B. 1/2 F
C. 2 F
D. 4 F
E. 16
F
Pembahasan
Diketahui :
Gaya tarik 1 (F1) = F
Pertambahan
panjang 1 (∆x1) = ∆L
Pertambahan panjang 2 (∆x2) = 0,5 ∆L
Ditanya
: Gaya tarik 2 (F2)?
Jawaban :
Rumus hukum Hooke :
F = k Δx
k = F / Δx
Batang yang digunakan sama sehingga konstanta
elastisitas (k) sama.
k1 = k2
F1 / ∆x1 = F2 / ∆x2
F /
ΔL = F2 / 0,5ΔL
F / 1 = F2 / 0,5
F = F2 /0,5
F2 = 0,5 F
Maka
besar gaya tariknya adalah 0,5F (B)
4. Sebuah batang baja
homogen panjang L, ketika ditarik dengan gaya F bertambah panjang sebesar
∆L. Tentukan pertambahan panjang dari batang baja, jika besar gaya tarik
yang dikeluarkan adalah 5 kali dari semula …
A. 1/4 ΔL
B. 1/2
ΔL
C. 2 ΔL
D. 5 ΔL
E. 16 ΔL
Pembahasan
Diketahui
:
Gaya tarik 1 (F1) = F
Gaya tarik 2 (F2) = 5 F
Pertambahan
panjang 1 (∆x1) = ∆L
Ditanya : Pertambahan panjang 2 (∆x2) =
?
Jawaban :
Rumus hukum Hooke :
F = k Δx
k = F / Δx
Batang yang digunakan sama sehingga konstanta
elastisitas (k) sama.
k1 = k2
F1 / ∆x1 = F2 / ∆x2
F /
ΔL = 5F / ∆x2
1 / ΔL = 5 / ∆x2
∆x2 = 5 ΔL
Maka besar
gaya tariknya adalah 5 ΔL (D)
5. Sebuah batang baja homogen
panjang L, ketika ditarik dengan gaya F bertambah panjang sebesar ∆L.
Tentukan pertambahan panjang dari batang baja, jika besar gaya tarik yang
dikeluarkan adalah 1/4 kali dari semula …
A. 1/4 ΔL
B. 1/2 ΔL
C.
2 ΔL
D. 5 ΔL
E. 16 ΔL
Pembahasan
Diketahui :
Gaya
tarik 1 (F1) = F
Gaya tarik 2 (F2) = 1/4 F=0,25 F
Pertambahan
panjang 1 (∆x1) = ∆L
Ditanya : Pertambahan panjang 2 (∆x2) =
?
Jawaban :
Rumus hukum Hooke :
F = k Δx
k = F / Δx
Batang yang digunakan sama sehingga konstanta
elastisitas (k) sama.
k1 = k2
F1 / ∆x1 = F2 / ∆x2
F /
ΔL = 0,25 F / ∆x2
1 / ΔL =0,25 / ∆x2
∆x2 = 0,25 ΔL
Maka
besar gaya tariknya adalah 0,25 ΔL (A)
6. Lima buah pegas
disusun seri. Berarti beban yang harus diberikan agar pertambahan panjang
pegas pada susunan seri sama dengan pertambahan panjang pegas tunggal
adalah.
A. 1/4 F
B. 1/2 F
C. 2 F
D. 4 F
E. 16
F
Pembahasan
Diketahui :
Lima buah pegas disusun
seri
Ditanya : beban yang harus diberikan agar pertambahan
panjang pegas pada susunan seri sama dengan pertambahan panjang pegas
tunggal (F) = ?
Jawaban :
Rumus hukum Hooke :
F = k Δx
∆x=F/k
Rumus Pegas Seri
1/ks = 1/k₁ + 1/k₂ +
1/k₃ + ... + 1/k₅
1/ks=(1/5)k1
∆x2 adalah pertambahan
panjang lima buah pegas seri
∆x1 adalah pertambahan panjang satu buah
pegas tunggal
∆x1 = ∆x2
F1 / k1 = F2 / (1/5)k1
F1
/1 = F2 / (1/5)
F1=5F2
F2=0,2 F1
Maka beban yang
harus diberikan pada pegas seri adalah 0,2 dari beban pada pegas tunggal
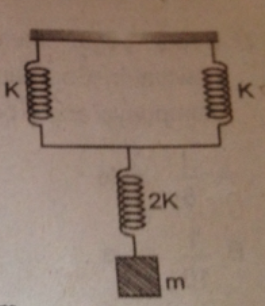
7. Soal UN 2009/2010 P70 No.05
Tiga pegas identik
dengan konstanta pegas masing-masing 200 N/m, disusun seperti gambar.
Ketika diberi beban 100 gram (percepatan gravitasi g = 10 m/s) maka
pertambahan panjang susunan pegas adalah…
A. x = 0,50 cm
B. x =
0,75 cm
C. x = 0,85 cm
D. x = 1,00 cm
E. x = 1,50 cm
Pembahasan
Diketahui :
Konstanta pegas(k) =k1=k2=k3=200 N/m
Massa
beban(m)=100 gram = 0,1 kg
Gravitasi (g) = 10 m/s
Berat beban
(w) = m g = (0,1)(10)=1 kg m/s² = 1 Newton
Ditanya :
Pertambahan panjang pegas (∆x) = ?
Jawaban :
Langkah 1: Menentukan Konstanta pegas pengganti
Pada gambar, pegas 2(k2) dan pegas 3(k3) tersusun secara paralel.
Oleh karena itu dapat dicari konstanta pegas pengganti:
kp=k2+k3
kp=200+200=400
N/m
Setelah didapatkan konstanta pegas pengganti, selanjutnya
mencari konstanta pegas pengganti antara pegas pengganti paralel (kp) dan
k1 yang tersusun secara seri
1/ks = 1/kp + 1/k1
1/ks =
1/400 + 1/200=1/400 + 2/400 = 3/400
ks= 400/3 N/m
Langkah 2: Menentukan pertambahan panjang pegas dengan hukum Hooke
Rumus hukum Hooke :
F = k Δx
Δx=F/k = w/k
Δx=1/(400/3)=3/400=0,0075
meter = 0,75 cm
Maka Pertambahan panjang pegas adalah 0,75 cm
(B)
8. Soal UN 2015
Tiga pegas disusun seperti
gambar berikut. Jika konstanta pegas k= 50 N/m dan pada susunan pegas
tersebut digantungkan beban 400 gram maka pertambahan panjang susunan
pegas adalah…
A. 2 cm
B. 4 cm
C. 8 cm
D. 16 cm
E.
50 cm
Diketahui :
k=k1=k2=50 N/m
k3=2k=2*50=100 N/m
Massa beban(m)=400 gram = 0,4 kg
Gravitasi (g) = 10 m/s
Berat beban (w) = m g = (0,4)(10)=4 kg m/s² = 4 Newton
Ditanya : Pertambahan panjang pegas (∆x) = ?
Jawaban :
Langkah 1: Menentukan Konstanta pegas pengganti
Pada gambar, pegas 1(k1) dan pegas 2(k2) tersusun secara paralel. Oleh karena itu dapat dicari konstanta pegas pengganti:
kp=k1+k2
kp=50+50=100 N/m
Setelah didapatkan konstanta pegas pengganti selanjutnya mencari konstanta pegas pengganti antara pegas pengganti paralel (kp) dan k3 yang tersusun secara seri,
1/ks = 1/kp + 1/k3
1/ks = 1/100 + 1/100=2/100 = 1/50
ks= 50 N/m
Langkah 2: Menentukan pertambahan panjang pegas dengan hukum Hooke
Rumus hukum Hooke :
F = k Δx
Δx=F/k = w/k
Δx=4/50=0,08 meter = 8 cm
Maka Pertambahan panjang pegas adalah 8 cm (C)
9. Perhatikan gambar sususan pegas disamping:
Jika k1=30 N/m, k2=40 N/m, k3=30 N/m, k4=100 N/m, k5=200 N/m dan F=200 N. Tentukan pertambahan panjang susunan pegas tersebut.
A. 2 m
B. 4 m
C. 8 m
D. 10 m
E. 5 m
Pembahasan
Diketahui :
k1 = 30 N/m
k2= 40 N/m
k3 = 30
N/m
k4 = 100 N/m
k5 = 200 N/m
F = 200 N
Gravitasi (g)
= 10 m/s
Ditanya : Pertambahan panjang pegas (∆x) = ?
Jawaban
:
Langkah 1: Menentukan Konstanta pegas pengganti
Pada
gambar, pegas 1(k1), pegas 2(k2) dan pegas 3(k3)tersusun secara paralel.
Oleh karena itu dapat dicari konstanta pegas pengganti:
kp = k1
+ k2 + k3
kp = 30 + 40 + 30
kp = 100 N/m
Setelah
didapatkan konstanta pegas pengganti selanjutnya mencari konstanta pegas
pengganti antara pegas pengganti paralel (kp), k4 dan k5 yang tersusun
secara seri,
1/ks = 1/kp + 1/k4 + 1/k5
1/ks = 1/100 +
1/100 + 1/200
1/ks = 2/200 + 2/200 + 1/200
1/ks = 5/200
ks
= 200/5
ks = 40 N/m
Langkah 2: Menentukan pertambahan panjang pegas dengan hukum Hooke
Rumus hukum Hooke :
F = k Δx
Δx=F/ks
Δx=200/40=5
meter
Maka Pertambahan panjang pegas adalah 5 m (E)
10.
Tiga pegas identik dengan konstanta 200 N/m disusun secara paralel. Anggap
susunan pegas hanya dipengaruhi oleh beban. Jika susunan pegas diberi
beban sehingga bertambah panjang 16 cm, tentukan pertambahan panjang
masing-masing pegas!
A. 1,22 cm
B. 2,54 cm
C. 3,68 cm
D.
4,46 cm
E. 5,33 cm
Pembahasan
Diketahui :
Konstanta
pegas (k) = 200N/m
Pertambahan panjang susunan (Δx) = 16 cm
Jumlah
pegas (n) = 3
Ditanya : Pertambahan panjang pegas masing-masing
pegas (∆x') = ?
Jawaban :
Dikarenakan konstanta pegas (k)
tetap, maka konstanta dapat diabaikan sehingga yang mempengaruhi hanyalah
beban. Sehingga:
∆x' = pertambahan panjang / jumlah pegas
∆x'
= ∆x/ n
∆x'= 16cm/3
∆x'= 16/3
∆x'= 5.33 cm
Maka
Pertambahan panjang masing-masing pegas adalah 5.33 cm (E)
11.
Dua Susunan pegas ditunjukkan pada gambar di samping. Perbandingan
pertambahan panjang susunan pegas (I) terhadap susunan pegas (II)
adalah...
A. 1 : 2
B. 2 : 1
C. 2 : 3
D. 3 : 4
E.
3 : 8
Pembahasan
Diketahui :
Konstanta pegas (k) = k
Pertambahan
panjang susunan (Δx) = Δx
Massa benda (m) = M
Ditanya :
Perbandingan pegas (I) terhadap pegas (II)
Jawaban :
Menentukan konstanta pengganti.
Pegas (I)
Susunan
paralel
kp=k1+k2=2k
Susunan seri
1/ks=1/kp + 1/k
1/ks=1/2k
+ 1/k
1/ks=1/2k + 2/2k=3/2k
ks1=2/3 k
Pegas (II)
Susunan
seri
1/ks=1/k + 1/k
1/ks=1/k + 1/k
1/ks=2/k
ks2=0,5
k
Menentukan perbandingan.
F = k Δx
Δx=F/k
Δx1/Δx2=F/ks1/(F2/ks2)
Δx1/Δx2=M/(2/3 k)/(M/1/2k)
Δx1/Δx2=M/(2/3 k)/(M/1/2k)
Δx1/Δx2=(3/2)(Mk/(2)(Mk)
Δx1/Δx2=3/4
Maka perbandingan pegas (I) dan pegas (II) adalah
3 : 4 (D)
12. Dua buah pegas di susun secara paralel,
masing-masing pegas konstanta 200 N/m. Jika pegas digantung massa 2 kg
tentukan:
A. Pertambahan panjang pegas.
B. Pertambahan panjang
pegas jika di susun seri.
Pembahasan
Diketahui :
Konstanta pegas (k) = 200 N/m
Massa
benda (m) = 2 kg
Gravitasi (g) = 10 m/s
Berat benda (w) = m g =
(2)(10) = 20 Newton
Ditanya :
A. Pertambahan panjang
pegas (Δx)
B. Pertambahan panjang pegas jika di susun seri(Δx')
Jawaban :
Menentukan konstanta pengganti.
Susunan paralel
kp=k1+k2=200
+ 200 =400 N/m
Susunan seri
1/ks=1/200 + 1/200
1/ks=2/200
1/ks=1/100
ks=100
Menentukan pertambahan panjang.
F = k Δx
Δx=F/k
Pertambahan panjang pegas (Δx) susunan paralel
Δx=F/k=w/k
Δx=20/400=0,05 m = 5 cm
Pertambahan panjang pegas (Δx) susunan seri
Δx=F/k=w/k
Δx=20/100=0,2 m = 20 cm
Maka petambahan
panjang pegas susunan paralel dan seri adalah 5 cm dan 20 cm.
13.
Tiga buah pegas identik dengan konstanta 1000 N/m. Susunan pegas di beri
beban sehingga bertambah panjang 6 cm ,maka pertambahan panjang masing
masing pegas adalah?
A. 1 cm
B. 2 cm
C. 3 cm
D. 4
cm
E. 5 cm
Pembahasan
Diketahui :
Konstanta
pegas (k) = 1000 N/m
Pertambahan panjang susunan (Δx) = 6 cm
Jumlah
pegas (n) = 3
Ditanya : Pertambahan panjang pegas masing-masing
pegas (∆x') = ?
Jawaban :
Dikarenakan konstanta pegas (k)
tetap, maka konstanta dapat diabaikan sehingga yang mempengaruhi hanyalah
beban. Sehingga:
∆x' = pertambahan panjang / jumlah pegas
∆x'
= ∆x/ n
∆x'= 6 cm/3
∆x'= 6/3
∆x'= 2 cm
Maka
Pertambahan panjang masing-masing pegas adalah 2 cm (B)
14.
Sepuluh pegas identik dipasang secara paralel. Berapakah berat beban yang
harus diberikan agar pertambahan panjang pegas pada susunan paralel sama
dengan pertambahan panjang pegas tunggal?
A. 1 cm
B. 2 cm
C.
3 cm
D. 4 cm
E. 5 cm
Pembahasan
Diketahui :
Konstanta
pegas (k)
Pertambahan panjang susunan (Δx)
Jumlah pegas (n) =
10
Ditanya : Berapakah berat beban yang harus diberikan agar
pertambahan panjang pegas pada susunan paralel sama dengan pertambahan
panjang pegas tunggal?
Jawaban :
Menentukan konstanta pengganti pegas paralel
kp=n k=10k
Menentukan perbandingan antara pegas paralel dan tunggal
F = k Δx
Δx=F/k=w/k
Δxparalel=Δxtunggal
wp/10k=wt/k
wp/wt=10k/k
wp/wt=10/1
wp
: wt = 10 : 1
Maka berat beban yang harus diberikan agar
pertambahan panjang pegas pada susunan paralel sama dengan pertambahan
panjang pegas tunggal adalah 10 kali berat beban awal.
15.
Sebuah pegas memiliki konstanta 100 N/m beban bermasa 5 kg digantungkan
sehingga pegas bertambah panjang. Tentukan
A. Konstanta susunan pegas?
B. Pertambahan panjang susunan pegas?
C.
Energi potensial?
Pembahasan
Diketahui :
Konstanta
pegas (k) = 100 N/m
Massa beban (m) = 5 kg
Gravitasi (g) = 10
m/s
Berat beban (w)= m g= (5)(10)=50 Newton
Ditanya :
A. Konstanta susunan pegas (k)?
B. Pertambahan panjang susunan
pegas (Δx)?
C. Energi potensial (Ep)?
Jawaban :
A. Konstanta susunan pegas (k)?
Konstanta pegas (k) = 100 N/m
B. Pertambahan panjang susunan pegas (Δx)?
F = k Δx
Δx=F/k=w/k
Δx=50/100= 0,5 m =50 cm
C. Energi potensial (Ep)?
Ep = 1/2 kΔx
Ep = (0,5)(100)(0,5)= 25 Joule
Maka
Konstanta susunan pegas (k), Pertambahan panjang susunan pegas (Δx) dan
Energi potensial (Ep) adalah 100 N/m, 0,5 m dan 25 Joule.
Dikarenakan
konstanta pegas (k) tetap, maka konstanta dapat diabaikan sehingga yang
mempengaruhi hanyalah beban. Sehingga:
∆x' = pertambahan
panjang / jumlah pegas
∆x' = ∆x/ n
∆x'= 6 cm/3
∆x'= 6/3
∆x'=
2 cm
Maka Pertambahan panjang masing-masing pegas adalah
2 cm (B)
16. Tiga pegas yang identik dengan konstanta
pegas 300 N/m yang diberi beban 200 gram. Tentukan penambahan panjang
susunan pegas tersebut bila pegas disusun secara seri maupun paralel.
Pembahasan
Diketahui :
Konstanta pegas (k) = 300 N/m
Massa
benda (m) = 200 g = 0,2 kg
Gravitasi (g) = 10 m/s
Berat benda
(w) = m g = (0,2)(10) = 2 Newton
Ditanya :
A. Pertambahan
panjang pegas jika di susun paralel(Δx)
B. Pertambahan panjang pegas
jika di susun seri (Δx')
Jawaban :
Menentukan konstanta pengganti.
Susunan paralel
kp=k1+k2+k3=
300 + 300 + 300 = 900 N/m
Susunan seri
1/ks=1/300 + 1/300
+ 1/300
1/ks=3/300
1/ks=1/100
ks=100
Menentukan pertambahan panjang.
F = k Δx
Δx=F/k
Pertambahan panjang pegas (Δx) susunan paralel
Δx=F/k=w/k
Δx=2/900=0,00222 m = 0,22 cm
Δx=F/k=w/k
Δx=2/100=0,02 m = 2 cm
Maka petambahan panjang pegas susunan paralel dan seri adalah 0,22 cm dan 2 cm.
17. Jika konstanta pegas k=60 N/m dan susunan pegas memiliki pertambahan
panjang 10 cm maka berat beban yang digantungkan pada susunan pegas
tersebut adalah.
A. 1 Newton
B. 2 Newton
C. 3 Newton
D.
4 Newton
E. 5 Newton
Pembahasan
Diketahui :
Konstanta pegas (k) = 60 N/m
Pertambahan
panjang (Δx) = 10 cm = 0,1 m
Ditanya :
Berat benda (w) =
?
Jawaban :
F = w = k Δx
w = (60) (0,1) = 6 Newton
Maka berat benda tersebut adalah 6 Newton.
18. Susunan pegas
terdiri dari dua pegas dengan konstanta masing masing 600 N/m dan 800 N/m.
jika pada ujung susunan tersebut diberi beban 100 N. tentukanlah
pertambahan panjang susunan pegas jika pegas pegas tersebut
A.
disusun seri
B. disusun paralel
Pembahasan
Diketahui :
Konstanta pegas (k1) = 600 N/m
Konstanta
pegas (k2) = 800 N/m
Berat benda (w) = 100 Newton
Ditanya
:
A. Pertambahan panjang pegas jika di susun seri (Δx)
B.
Pertambahan panjang pegas jika di susun paralel (Δx')
Jawaban :
Menentukan konstanta pengganti.
Susunan paralel
kp=k1+k2=
600 + 800 = 1400 N/m
Susunan seri
1/ks=1/600 + 1/800
1/ks=7/2400
ks=2400/7
Menentukan pertambahan panjang.
F = k Δx
Δx=F/k
Pertambahan panjang pegas (Δx) susunan seri
Δx=F/k=w/k
Δx=100/1400=0,07 m= 7 cm
Δx=F/k=w/k
Δx=100/(2400/7) =0,29 m = 29 cm
Maka petambahan panjang pegas susunan seri dan paralel adalah 7 cm dan 29 cm.
19. Bila dua buah pegas identik disusun seri dan diberi beban 5 kg pada
ujungnya, maka akan bertambah panjang 10 cm. Jika kedua pegas disusun
pararel dan di gantungkan beban yang sama, maka akan bertambah panjang ?
Pembahasan
Diketahui :
Konstanta pegas (k)
Pertambahan
panjang pegas jika di susun seri (Δx) = 10 cm = 0,1 m
Massa bendan
(m) = 5 kg
Gravitasi (g) = 10 m/s
Berat benda (w) = m g =
(5)(10) = 50 Newton
Ditanya :
Pertambahan panjang pegas
jika di susun paralel (Δx')
Jawaban :
Menentukan konstanta pengganti susunan pegas seri.
F = w =
ks Δx
50 = ks Δx
50 = ks (0,1)
ks = 50/0,1 = 500 N/m
Menentukan konstanta pegas.
1/ks = 1/k1 + 1/k2
1/500 = 1/k + 1/k
1/500 = 2/k
k
/2= 500
k = 1000 N/m
Menentukan konstanta pengganti susunan pegas paralel.
kp = k1 + k2
kp = 1000 + 1000
kp = 2000 N/m
Menentukan pertambahan panjang
F = w = kp Δx'
50 = kp Δx'
50 = (2000)
Δx'
Δx'= 50/2000
Δx' = 0,025 m = 2,5 cm
Maka petambahan panjang pegas susunan paralel adalah 2,5 cm
20.
Tiga buah pegas masing-masing memiliki konstanta pegas 600 N/m disusun
seperti gambar dibawah. Jika susunan pegas ditarik dengan gaya F= 1,6 N.
Berapa pertambahan panjang susunan pegas tersebut
Pembahasan
Diketahui :
Konstanta pegas (k) =600 N/m
Gaya Tarik (F) = 1,6 Newton
Ditanya :
Pertambahan panjang pegas (Δx)
Jawaban :
Menentukan konstanta pengganti susunan pegas paralel.
kp = k1
+ k2
kp = 600 + 600
kp = 1200 N/m
Menentukan konstanta pegas gabungan yang tersusun secara seri.
1/ks = 1/kp + 1/k3
1/ks = 1/1200 + 1/600
1/ks= 3/1200
=1/400
ks= 400 N/m
Menentukan pertambahan panjang
F = ks Δx
Δx=F/k
Δx=1,6/400= 0,004 m = 0,4
cm
21. UN 2007/2008
Pada percobaan elastisitas suatu pegas diperoleh
data seperti tabel di bawah ini. Dapat disimpulkan bahwa nilai konstanta
pegas tersebut adalah….
Gaya (N) Pertambahan Panjang (m)
0,98 8.10^(-4)
1,96 16.10^(-4)
2,94 24.10^(-4)
3,92 32.10^(-4)
A. 1002 N/m
B. 1201 N/m
C. 1225 N/m
D.
1245 N/m
E. 1250 N/m
Pembahasan
Diketahui :
Gaya Tarik (F) = 0,98
N,
1,96 N, 2,94 N, 3,92 N
Pertambahan panjang pegas (Δx) = 8.10^(-4) m, 16.10^(-4) m, 24.10^(-4) m, 32.10^(-4) m
Ditanya :
Konstanta pegas (k)
Jawaban :
Menentukan konstanta pegas
F = k Δx
k=F/Δx
*Pada soal seperti ini, cukup mengunakan salah satu sampel saja. Tetapi
bila ragu dapat dikerjakan semuanya.
k1=F1/Δx1= 0,98/(8.10^(-4)) = 1225 N/m
k2=F2/Δx2= 1,96/(16.10^(-4)) = 1225 N/m
k3=F3/Δx3= 2,94/(24.10^(-4)) = 1225 N/m
k4=F4/Δx4= 3,92/(32.10^(-4)) = 1225 N/m
22. Dalam persamaan osilasi pegas, ada konstanta pegas yang
mempengaruhi. Jelaskan bagaimana pengaruh konstanta pegas ?
Jawaban
Konstanta pegas merupakan suatu konstanta yang
mewakili tingkat kelenturan suatu pegas. Contohnya, suatu pegas yang sulit
diregangkan (kaku) memiliki nilai konstanta pegas yang lebih besar, hal
ini dikarenakan gaya yang dibutuhkan untuk menyebabkan pegas bertambah
panjang menjadi lebih besar. Begitupun sebaliknya, pegas yang mudah
diregangkan (lentur) memiliki nilai konstanta pegas yang lebih kecil.
Persamaannya
Hukum Hooke:
F = k . Δx
dimana
F = Gaya (Newton)
k
= Konstanta pegas (Newton/ meter)
Δx = Pertambahan panjang pegas
(meter)
23. Pegas tiga buah, dengan konstanta yang sama disusun
secara paralel konstanta pegas masing masing 30 N/m. Berapakah konstanta
total ke tiga pegas tersebut
a. 30 N/m
b. 45 N/m
c. 60
N/m
d. 90 N/m
e. 105 N/m
Pembahasan
Diketahui :
Konstanta pegas (k)=k1=k2=k3 = 30 N/m
Ditanya
:
Konstanta pegas pengganti susunan paralel (kp)
Jawaban
:
Susunan paralel
kp=k1+k2=k3= 30+30+30 = 90 N/m
Jadi konstanta penggantinya adalah 90 N/m (d)
23. Jika
masing-masing pegas mempunyai konstanta pegas sama yaitu 250 N/m. Tentukan
konstanta gabungan susunan pegas tersebut secara paralel maupun seri.
a.
250 dan 250
b. 250 dan 125
c. 500 dan 125
d. 500 dan 500
e.
125 dan 500
Pembahasan
Diketahui :
Konstanta pegas (k) =250 N/m
Ditanya :
Konstanta gabungan pegas paralel (kp) maupun
seri (ks)
Jawaban :
kp = k1 + k2
kp = 250 + 250
kp = 500 N/m
Menentukan konstanta pegas gabungan yang tersusun secara seri.
1/ks = 1/k1 + 1/k2
1/ks = 1/250 + 1/250
1/ks= 2/250 =1/125
ks= 125 N/m
Maka didapat konstanta pegas tersebut adalah 500 N/m untuk susunan
paralel dan 125 N/m untuk susunan seri. (C)
24. Empat buah
pegas yang sama dengan konstanta pegas = k dirangkai paralel. Konstanta
rangkaian pegas tersebut adalah
Jawaban :
Menentukan konstanta pengganti susunan pegas paralel.
kp = k
+ k + k + k
kp = 4 k
Maka konstanta pegas tersebut adalah
4k
25. Enam buah pegas identik tiga dipasang paralel dan tiga
dipasang seri. Bila konstanta pegas sama dengan k, maka besar konstanta
pengganti adalah
a. 0,3 k
b. 0,6 k
c. 0,9 k
d. 1,2
k
e. 1,5 k
Pembahasan
Diketahui :
Konstanta pegas =k
Ditanya :
Konstanta pengganti??
Jawaban :
Menentukan konstanta pengganti susunan pegas paralel.
Untuk menghitung total konstanta pengganti, terlebih dahulu kita hitung
konstanta pengganti untuk rangkaian pegas paralel. Karena pegas identik,
maka rumusnya adalah
kp = n. k
kp = 3. k
kp = 3k
Menentukan konstanta pegas tersusun secara seri.
Selanjutnya kita hitung konstanta pegas pengganti untuk rangkaian
pegas seri. Karena pegas identik, maka rumusnya adalah
ks = k /
n
ks = k / 3
Selanjutnya barulah kita hitung total
konstanta pengganti untuk kedua rangkaian. Kedua rangkaian ini disusun
secara seri, sehingga
1/kt = 1/ks + 1/Kp
1/kt = 3/k +
1/3k
1/kt = 9/3k + 1/3k
1/kt = 10/3k
kt = 3k / 10
kt =
0,3 k
Jadi, besar konstanta pengganti adalah 0,3 k
(a)
26. Sebuah pegas yang digantung vertikal memiliki panjang
80 cm. Sebuah beban seberat 100 N digantungkan pada pegas tersebut
sehingga panjangnya bertambah jadi 100 cm. Berapakah besarnya nilai
tetapan pegas? Jika diberi beban sebesar 75 N, berapa panjang pegas
tersebut
Pembahasan
Diketahui :
Panjang awal =
80 cm.
w = 100 Newton
Panjang akhir = 100 cm.
Ditanyakan
:
a. Besar nilai tetapan/ konstanta pegas (k) = ?
b. Panjang pegas jika diberi beban sebesar 75 N
Jawaban
a.
Besar nilai tetapan pegas
Menentukan pertambahan panjang pegas (Δx):
Δx= 100 - 80 = 20 cm = 0,2 m
Menentukan nilai tetapan pegas (k) :
F = k Δx
k=F/Δx= w/Δx
k = 100 / 0,2
k = 500 N/m
Jadi, besar tetapan
pegasnya adalah 500 N/m.
b. Panjang pegas jika diberi beban
sebesar 75 N
F = w = k Δx
Δx = w / k
Δx
= 75/ 500
Δx = 0,15 m = 15 cm
Sehingga panjang pegas
menjadi
∑x = x + Δx
∑x = 80 cm + 15 cm
∑x
= 95 cm
Jadi, panjang pegas tersebut bila diberi gaya sebesar
75 N adalah 95 cm.
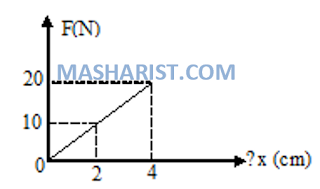
27. Gambar dibawah menunjukkan grafik
hubungan antara gaya (F) dengan pertambahan panjang pegas (∆x). Tentukan
konstanta Pegas.
Pembahasan
Diketahui :
F1=10 N
F2=20 N
Δx1=2 cm – 0
cm= 2 cm =0,02 m
Δx2=4 cm – 0 cm= 4 cm =0,04 m
Ditanya
: Konstanta (k)?
Jawaban :
28. Dalam suatu praktikum untuk menentukan konstanta suatu pegas
diperoleh data sebagaimana dibawah. Jika F adalah gaya dan ∆x adalah
pertambahan panjang pegas, tentukan nilai konstanta pegasnya
Pembahasan
Diketahui : (lihat Tabel), nilai 1 cm =0,01 m
Ditanya
: k=…
Jawaban :
Maka konstanta pegas dari grafik diatas adalah 500 N/m.
29. Suatu pegas akan bertambah panjang 10 cm jika diberi gaya 30 N.
Pertambahan panjang pegas jika diberi gaya 21 N adalah...
Pembahasan
Diketahui
:
F1=30 N
F2=21 N
Δx1=10 cm =0,1 m
Ditanya :
Pertambahan
panjang pegas Δx2 =?
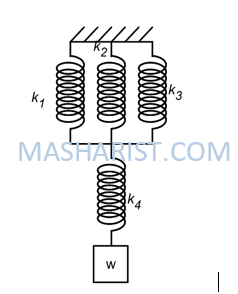
30. Perhatikan gambar dibawah. Tentukan nilai w, jika diketahui konstata
masing-masing pegas adalah k1=k2=k3=k4=200 N/m. Bila diketahui pertambahan
panjang pegas adalah 4 cm.
Pembahasan
Diketahui :
Konstanta masing-masing pegas (k1
= k2 = k3= k4 )= 200 N/m
Pertambahan panjang sistem pegas (x) = 4 cm
= 0,04 meter
Ditanya : berat beban (w)
Jawaban :
Terlebih
dahulu hitung konstanta pegas gabungan yang disusun paralel.
Konstanta
pegas penggantinya adalah :
kp = k1 + k2 + k3 = 200 + 200 + 200
= 600 N/m
Sehingga gambar pada soal menjadi.
3. Hukum Hooke Energi Potensial Pegas
Energi Potensial Pegas serta Keterangannya
Ep = ¹/₂ k Δx²
atau
Ep = ¹/₂ F Δx
Dimana :
Ep = Energi Potensial
Pegas (Joule)
k = konstanta pegas (Newton/meter)
Δx
= pertambahan pnjang pegas (meter)
F = Gaya Pegas (Newton)
Contoh Soal Energi Potensial Pegas
1.
Sebuah pegas memiliki energi potensial sebesar 27 Joule ketika bertambah
panjang 3 cm. Besar energi potensial pegas ketika bertambah panjang 5 cm
adalah ?
a. 75 Joule
b. 76 Joule
c. 77 Joule
d. 78
Joule
e. 79 Joule
Pembahasan
Diketahui :
Energi Potensial Awal (Ep1) = 27
Joule
Pertambahan panjang awal (Δx1) = 3 cm = 0,03 m
Ditanya
:
Energi Potensial Akhir (Ep2) bila Pertambahan panjang (Δx2) = 5 cm
Jawaban :
Ep1/Ep2=(¹/₂ k Δx1²)/(¹/₂ k
Δx2²)
*Nilai yang sama dieliminasi/dicoret yaitu nilai ¹/₂ k
hal ini dikarenkan pegas memiliki konstanta yang sama, sehingga persamaan
diatas menjadi
27/Ep2=(0,03²)/(0,05²)
Ep2=(27)(0,05²)/(0,03²)=75
Joule
Maka nilai Energi Potensial saat pertambahan panjang 5 cm
adalah 75 Joule (a)
2. Gaya sebesar 800 N dapat meregangkan
sebuah pegas sehingga 0,2 meter. Berapakah energi potensial pegas itu jika
diregangkan 0,2 meter dan Berapakah energi potensialnya jika pegas itu di
tekan 5 cm ?
Pembahasan
Diketahui :
F = 800 N
Pertambahan
panjang (Δx) = 0,2 meter
Ditanya :
a. Energi Potensial
(Ep) bila Pertambahan panjang (Δx) = 0,2 m
b. Energi Potensial (Ep)
bila ditekan (Δx') = - 5 cm
Jawaban :
Langkah 1: Menentukan konstanta pegas
F = k
Δx
k = F/Δx
k= 800/0,2
k= 4000 N/m
Langkah 2 : Energi Potensial (Ep) bila Pertambahan panjang (Δx) = 0,2 m
a.
Ep = ¹/₂ k Δx²
Ep = ¹/₂ (4000) (0,2)²
Ep = 80 Joule
Langkah 3 : Energi Potensial (Ep) bila ditekan (Δx') = - 5 cm = 0,05 m
b.
Ep = ¹/₂ k Δx²
Ep = ¹/₂ (4000) (0,05)²
Ep = 5
Joule
Maka nilai Energi Potensial saat pertambahan panjang 0,2
m dan ditekan 5 cm adalah 80 Joule dan 5 Joule.
3. Pegas dengan konstanta pegas 600 N/m. Digantungi beban sehingga pegas
teregang sepanjang 20 cm. Energi potensial pegas itu adalah
a. 11
Joule
b. 12 Joule
c. 13 Joule
d. 14 Joule
e. 15
Joule
Diketahui :
Konstanta pegas (k) = 600 N/m
Pertambahan panjang (Δx) = 20 cm = 0,2 meter
Ditanya :
Energi Potensial (Ep) bila Pertambahan panjang (Δx) = 20 cm
Jawaban :
Energi Potensial (Ep) bila Pertambahan panjang (Δx) = 0,2 m
Ep = ¹/₂ k Δx²
Ep = ¹/₂ (600) (0,2)²
Ep = 12 Joule
Maka nilai Energi Potensial saat pertambahan panjang 20 cm adalah 12 Joule (b)
4. Pegas memiliki Energi Potensial sebesar 125 Joule saat meregang sejauh
5 cm. Saat meregang sejauh 4 cm, Energi Potensial Pegas sebesar ?
a.
75 Joule
b. 76 Joule
c. 80 Joule
d. 88 Joule
e. 89
Joule
Pembahasan
Diketahui :
Energi Potensial Awal
(Ep1) = 125 Joule
Pertambahan panjang awal (Δx1) = 5 cm = 0,05 m
Ditanya
:
Energi Potensial Akhir (Ep2) bila Pertambahan panjang (Δx2) = 4 cm
Jawaban :
Ep1/Ep2=(¹/₂ k Δx1²)/(¹/₂ k Δx2²)
*Nilai
yang sama dieliminasi/dicoret yaitu nilai ¹/₂ k hal ini dikarenkan pegas
memiliki konstanta yang sama, sehingga persamaan diatas menjadi
125/Ep2=(0,05²)/(0,04²)
Ep2=(125)(0,04²)/(0,05²)=80
Joule
Maka nilai Energi Potensial saat pertambahan panjang 4 cm
adalah 80 Joule (c)
5. Sebuah pegas memiliki energi potensial
sebesar 27 Joule ketika bertambah panjang 3 cm. Tentukan pertambaha
panjang pegas bila besar energi potensial pegas adalah 75 Joule?
a. 5
cm
b. 6 cm
c. 7 cm
d. 8 cm
e. 9 cm
Pembahasan:
Diketahui :
Energi Potensial Awal (Ep1) = 27 Joule
Energi
Potensial Awal (Ep2) = 75 Joule
Pertambahan panjang awal (Δx) = 3 cm
= 0,03 m
Ditanya :
Pertambahan panjang (Δx') = .. cm ?
Jawaban :
Ep1/Ep2=(¹/₂ k Δx²)/(¹/₂ k Δx'²)
*Nilai
yang sama dieliminasi/dicoret yaitu nilai ¹/₂ k hal ini dikarenkan pegas
memiliki konstanta yang sama, sehingga persamaan diatas menjadi
27/75=(0,03²)/(Δx'²)
Δx'=0,05
m = 5 cm
Maka nilai Energi Potensial saat 75 Joule mengalami
pertambahan panjang sebesar 5 cm (a)
6. Pegas dengan konstanta
pegas 600 N/m. Digantungi beban sehingga pegas teregang. Bila Energi
potensial pegas itu adalah 12 Joule, tentukan pertambahan panjangnya
a.
10 cm
b. 12 cm
c. 14 cm
d. 16 cm
e. 20 cm
Diketahui :
Konstanta pegas (k) = 600 N/m
Energi Potensial (Ep)= 12 Joule
Ditanya :
Pertambahan panjang (Δx)=?
Jawaban :
Energi Potensial (Ep) bila Pertambahan panjang (Δx) = 0,2 m
Ep = ¹/₂ k Δx²
12 = ¹/₂ (600) Δx²
Δx= √ (12/300) = 0,2 m =20 cm
Maka nilai pertambahan panjang adalah 20 cm (e)
7. Sebuah pegas pada saat ditarik dengan gaya tertentu, bertambah panjang
x dan energi potensialnya saat itu adalah E. Jika pegas tersebut ditarik
dengan gaya lain sehingga bertambah panjang 2x, maka energi potensial saat
itu adalah
a. E
b. 2E
c. 3E
d. 4E
e. 5E
Pembahasan
Diketahui
:
Energi Potensial awal (Ep)=E
Pertambahan panjang awal
(Δx)=x
Ditanya :
Energi Potensial Akhir (Ep2) bila
bertambah panjang 2x =?
Jawaban :
Ep1/Ep2=(¹/₂ k Δx1²)/(¹/₂ k Δx2²)
*Nilai yang sama
dieliminasi/dicoret yaitu nilai ¹/₂ k hal ini dikarenkan pegas memiliki
konstanta yang sama, sehingga persamaan diatas menjadi
E/Ep2=(x²)/((2x)²)
Ep2=(E)(4x²)/(x²)=4E
Maka
nilai Energi Potensial saat pertambahan panjang 2x adalah 4E (d)
8.
Sebuah pegas ketika ditarik dengan gaya 10 N pegas bertambah panjang 4 cm.
Berapa energi potensial pegas pada saat itu?
a. 0,1 Joule
b. 0,2
Joule
c. 0,3 Joule
d. 0,4 Joule
e. 0,5 Joule
Pembahasan
Diketahui
:
F = 10 N
Pertambahan panjang (Δx) = 4 cm = 0,04 meter
Ditanya
: Energi Potensial (Ep)
Jawaban :
Langkah 1: Menentukan konstanta pegas
F = k
Δx
k = F/Δx
k= 10/0,04
k= 250 N/m
Langkah 2 : Energi Potensial (Ep)
Ep = ¹/₂ k Δx²
Ep = ¹/₂
(250) (0,04 )²
Ep = 0,2 Joule
Maka nilai Energi Potensial
nya adalah 0,2 Joule(b)
9. Hitung energi potensial dari suatu
pegas dan yang konstanta pegasnya 100 N/m, jika pegas tersebut terengang
sepanjang 5 cm?
a. 0,125 Joule
b. 0,225 Joule
c. 0,325
Joule
d. 0,425 Joule
e. 0,525 Joule
Pembahasan
Diketahui
:
Konstanta pegas (k) = 100 N/m
Pertambahan panjang (Δx) = 5 cm
= 0,05 meter
Ditanya :
Energi Potensial (Ep) bila
Pertambahan panjang (Δx) = 5 cm = 0,05 meter
Jawaban :
Ep = ¹/₂ k Δx²
Ep = ¹/₂ (100) (0,05)²
Ep = 0,125 Joule
Maka nilai Energi Potensial adalah 0,125 Joule (a)
10.
Sebuah pegas ditarik dengan gaya 40 N pegas bertambah panjang sebesar 2
cm, maka energi potensial pegas adalah
a. 0,1 Joule
b. 0,2
Joule
c. 0,3 Joule
d. 0,4 Joule
e. 0,5 Joule
Pembahasan
Diketahui
:
Gaya Tarik (F) = 40 N
Pertambahan panjang (Δx) = 2 cm = 0,02
meter
Ditanya :
Energi Potensial (Ep) bila Pertambahan
panjang (Δx) = 2 cm = 0,02 meter
Jawaban :
Ep = ¹/₂ F Δx
Ep = ¹/₂ (40) (0,02)
Ep = 0,4 Joule
Maka nilai Energi Potensial adalah 0,4 Joule (d)
11.
Saat pegas ditarik oleh gaya 30 N energi potensial pegas menjadi 0,60
Joule. Konstanta pegas tersebut adalah
a. 250 N/m
b. 550 N/m
c. 750 N/m
d. 950 N/m
e. 1150 N/m
Pembahasan
Diketahui :
Gaya Tarik (F) =
30 N
Energi Potensial (Ep) = 0,60 Joule
Ditanya :
Konstanta (k)=?
Jawaban :
Langkah 1: Mencari pertambahan panjang (Δx)
Ep = ¹/₂ F Δx
0,6
= ¹/₂ (30) Δx
Δx = 0,04 m
Langkah 2 : Mencari nilai Konstanta (K)
F= k Δx
30 = (k) (0,04)
k = 750 N/m
Maka
nilai Konstanta pegas tersebut adalah 750 N/m (c)
13. Sebuah
pegas ditarik gaya 50 Newton, pegas bertambah panjang 3 cm, maka energi
potensial pegas adalah
a. 0,71 Joule
b. 0,72 Joule
c. 0,73
Joule
d. 0,74 Joule
e. 0,75 Joule
Pembahasan
Diketahui
:
Gaya Tarik (F) = 50 N
Pertambahan panjang (Δx) = 3 cm = 0,03
meter
Ditanya :
Energi Potensial (Ep)
Jawaban
:
Ep = ¹/₂ F Δx
Ep = ¹/₂ (50) (0,03)
Ep
= 0,75 Joule
Maka nilai Energi Potensial adalah 0,75 Joule
(e)
14. Sebuah pegas ditarik dengan 60 N sehingga bertambah
panjang 2 cm. Besar energi potensial pegas adalah
a. 0,70 Joule
b.
0,60 Joule
c. 0,50 Joule
d. 0,40 Joule
e. 0,30 Joule
Pembahasan
Diketahui
:
Gaya Tarik (F) = 60 N
Pertambahan panjang (Δx) = 2 cm = 0,02
meter
Ditanya :
Energi Potensial (Ep)
Jawaban
:
Ep = ¹/₂ F Δx
Ep = ¹/₂ (60) (0,02)
Ep
= 0,60 Joule
Maka nilai Energi Potensial adalah 0,60 Joule
(b)
15. Sebuah pegas ketika ditarik dengan gaya 100 N bertambah
2 cm. Berapa besar Energi Potensial Pegas saat itu
a. 1,00 Joule
b.
0,80 Joule
c. 0,60 Joule
d. 0,40 Joule
e. 0,20 Joule
Pembahasan
Diketahui
:
Gaya Tarik (F) = 100 N
Pertambahan panjang (Δx) = 2 cm = 0,02
meter
Ditanya :
Energi Potensial (Ep)
Jawaban
:
Ep = ¹/₂ F Δx
Ep = ¹/₂ (100) (0,02)
Ep
= 1 Joule
Maka nilai Energi Potensial adalah 1 Joule (a)
16.
Sebuah pegas di tarik dengan gaya 80 N hingga bertambah panjang 4 cm.
Energi Potensial Pegas tersebut adalah
a. 2,00 Joule
b. 1,80
Joule
c. 1,60 Joule
d. 1,40 Joule
e. 1,20 Joule
Pembahasan
Diketahui
:
Gaya Tarik (F) = 80 N
Pertambahan panjang (Δx) = 4 cm = 0,04
meter
Ditanya :
Energi Potensial (Ep)
Jawaban
:
Ep = ¹/₂ F Δx
Ep = ¹/₂ (80) (0,04)
Ep
= 1,6 Joule
Maka nilai Energi Potensial adalah 1,6 Joule
(c)
17. Pegas A memiliki konstanta sebesar k dan pegas B
memiliki konstanta pegas sebesar 3k maka. Kedua pegas diregangkan sejauh
d. Maka...
a. Energi potensial pegas A = energi potensial pegas B
b.
Energi potensial pegas A < energi potensial pegas B
c. Energi
potensial pegas A > energi potensial pegas B
d. Energi potensial
pegas A ⩽ energi potensial pegas B
e. Energi potensial pegas A ⩾
energi potensial pegas B
Pembahasan
Diketahui :
Energi
Potensial A (Ep)=EpA
Energi Potensial B (Ep)=EpB
Regangan
(Δx)=d
Konstanta pegas A = k
Konstanta pegas B = 3k
Ditanya :
Perbandingan?
Jawaban :
EpA/EpB=(¹/₂ k d²)/(¹/₂ 3k d²)
*Nilai yang sama
dieliminasi/dicoret yaitu nilai ¹/₂ k dan d hal ini
dikarenakan pegas memiliki konstanta yang sama, sehingga persamaan diatas
menjadi
EpA/EpB=1/3
Sehingga perbandingan Energi
Potensial Pegas A dan Energi Potensial Pegas B adalah 1 : 3, maka jawaban
yang tepat adalah (b)
Maka nilai Energi Potensial saat
pertambahan panjang 2x adalah 4E (d)
18. Pegas yang
direnggangkan dengan gaya 5 N menyimpan Energi Potensial Pegas 1 Joule.
Berapakah Energi Potensial Pegas jika direnggangkan dengan gaya 20 N?
a. 10 Joule
b. 8 Joule
c. 6 Joule
d. 4 Joule
e.
2 Joule
Pembahasan
Diketahui :
Gaya Tarik (F1) = 5
N
Gaya Tarik (F2) = 20 N
Energi Potensial (Ep1) = 1 Joule
Ditanya
:
Energi Potensial (Ep2) =?
Jawaban :
Ep = ¹/₂ F Δx
Ep1/Ep2 = (¹/₂ F1 Δx)/(¹/₂ F2 Δx)
*Nilai yang sama dieliminasi/dicoret yaitu nilai
¹/₂ dan Δx sehingga persamaan diatas menjadi
1/Ep2=5/20
5Ep2
= 20
Ep2=20/5=4 Joule
Maka nilai Energi Potensial adalah 4
Joule (d)
19. Suatu pegas meregang hingga energi potensialnya
200 Joule. Jika pegas tersebut kemudian ditarik hingga energi potensialnya
320 Joule, Besarnya usaha yang dikerahkan untuk menarik pegas tersebut
adalah
a. 120 Joule
b. 128 Joule
c. 126 Joule
d. 124
Joule
e. 122 Joule
Pembahasan
Diketahui :
Energi
Potensial (Ep1) = 200 Joule
Energi Potensial (Ep2) = 320 Joule
Ditanya
:
Usaha (W) =?
Jawaban :
W= ΔEp
W= Ep2-Ep1
W= 320-200=120 Joule
Maka besarnya usaha adalah 120 Joule (a)
20. Persamaan
Energi Potensial Pegas dirumuskan Ep = ½ k Δx² Dimana Ep = Energi
potensial pegas k = konstanta pegas Δx = pertambahan panjang pegas.
Tuliskan Dimensi dari Energi Potensial dan Konstanta Pegas!
Pembahasan
Diketahui
:
Ep = ½ k Δx²
Ditanya :
Dimensi dari Energi
Potensial dan Konstanta Pegas
Jawaban :
a. Energi Potensial
Ep = ½ k Δx²
Ep = (N/m) . m²
Ep=
(kg m/s²m) . m²
= kg m² s⁻²
Ep = [M]
[L]² [T]⁻²
b) Konstanta pegas
k = F / Δx
k = N / m
k = kg m/s²m
k = kg
. s⁻²
k = [M] [T]⁻²
4. Elastis dan Plastis
Contoh Soal Elastis dan Plastis
1. Soal UN Fisika SMA/MA 2013/2014 No.11
Perhatikan grafik
hubungan gaya ΔF dengan pertambahan panjang Δx pada suatu pegas di bawah!
Berdasarkan grafik, maka pegas tetap akan bersifat elastis pada gaya tarik
sebesar
A. 0 sampai 4 N
B. 0 sampai 8 N
C. 0 sampai 12 N
D. 8 N sampai 12 N
E. 8 N sampai 16 N
Pembahasan
Langkah 1 : Menentukan Elastitisas dari pegas dengan Hukum Hooke.
Perlu diingat pegas akan tetap bersifat elastis jika pada pegas tersebut masih berlaku hukum Hooke. Hukum Hooke dinyatakan melalui rumus :
k = ΔF / Δx
Keterangan rumus :
k = konstanta elastisitas, ΔF = gaya, Δx = panjang pegas
Hukum Hooke menyatakan bahwa perbandingan perubahan gaya (ΔF) terhadap perubahan panjang (Δx) pegas, selalu bernilai konstan.
Jika nilai k berubah maka hukum Hooke tidak lagi berlaku pada pegas dan hal ini menunjukkan bahwa pegas tidak lagi bersifat elastis.
Amati grafik di atas dan pahami perhitungan berikut ini.
k1 = ΔF / Δx = 4 / 2 = 2
k2 = ΔF / Δx = 8 / 4 = 2
k3 = ΔF / Δx = 12 / 7 = 1,7
Konstanta (k) pegas bernilai konstan hingga gaya tarik sebesar 8 Newton.
Jadi pegas tetap akan bersifat elastis pada gaya tarik sebesar 0 sampai 8 Newton atau di soal dapat dilihat dengan titik p (B)
5. Soal Latihan Hukum Hooke
1. Sebuah pegas homogen dengan konstanta pegas k dipotong menjadi 2 bagian sama panjang, kemudian pegas baru tersebut disusun secara paralel. Tentukan berapakah pertambahan panjang pegas tersebut? bila pertambahan panjang mula-mula adalah y.2. Empat buah pegas sejenis dengan dengan konstanta 200 N/m disusun secara seri. susunan tersebut digantungi benda bermassa 2 kg. hitunglah : a) pertambahan panjang susunan pegas
b) pertambahan panjang masing-masing pegas
3. Tiga buah pegas disusun secara seri dan paralel jika beban M digantung pada pegas ketiga pegas secara paralel, makaa pegas tersebut bertambah panjang 2 cm. Berapa pertambahan panjang susunan pegas bila disusun secara seri?
4. Dua pegas identik yang disusun paralel bertambah panjang 5 cm saat beban 2 kg digantungkan pada susunan tersebut. Jika sebuah pegas lain yang identik diparalelkan dengan kedua pegas terdahulu kemudian digantungkan beban 2 kg. Maka masing-masing pegas akan bertambah panjang... cm
5. Dua pegas A dan B panjangnya 40 cm dan 80 cm ditarik dengan gaya yang sama. Jika konstanta pegas A dan B masing masing 2k dan k dan pertambahan panjang pegas B adalah 0,2 cm, tentukan pertambahan panjang pada pegas A
6. Lima buah pegas spiral. Jika konstanta pegasnya k maka Tentukanla konstanta pegas susunan pegas tersebut bila pegas disusun secara paralel dan seri.
7. Energi potensial pegas ketika di tarik sehingga memendek sepanjang 7 cm adalah 800 Joule. Pegas harus ditekan berapa cm lagi supaya energi potensial menjadi 2400 joule
8. Ketika digantungi beban 2 kg, sebuah pegas memiliki energi potensial 0,2 joule. Pernyataan yang tepat ketika pegas memiliki energi potensial 2,00 joule adalah
9. Sebuah pegas dengan tetapan gaya k jika diregangkan sehingga mengalami pertambahan panjang sebesar x maka pegas tersebut menyimpan energi potensial yang nilainya ditentukan oleh nilai k dan nilai x. Dengan menggunakan konsep dimensi buatlah persamaan yang benar dari energi potensial pegas
10. Sebuah pegas tanpa beban panjangnya 30 cm pada pegas di beri baban 0.2kg. Panjang pegas menjadi 45 cm. Tentukan energi potensial pegas
11.UN 2000/2001
Batang serba sama (homogen) panjang L, ketika ditarik dengan gaya F bertambah panjang sebesar ∆L.
Agar pertambahan panjang menjadi 4 ∆L maka besar gaya tariknya adalah …
A. 1/4 F
B. 1/2 F
C. 2 F
D. 4 F
E. 16 F
12. UN 2009/2010
Tiga pegas identik dengan konstanta pegas masing-masing 200 N/m, disusun seperti gambar. Ketika diberi beban 100 gram (percepatan gravitasi g = 10 m/s) maka pertambahan panjang susunan pegas adalah…
A. x = 0,50 cm
B. x = 0,75 cm
C. x = 0,85 cm
D. x = 1,00 cm
E. x = 1,50 cm
13. UN 2008/2009
Tiga buah pegas dirangkai seperti gambar berikut ini. Jika konstanta pegas k1 = k2 = 3 Nm−1 dan k3 = 6 Nm−1, konstanta susunan pegas besarnya…..
A. 1 Nm−1
B. 3 Nm−1
C. 7,5 Nm−1
D. 12 Nm−1
E. 15 Nm−1
14. 10 buah pegas disusun seri. Berarti beban yang harus diberikan agar
pertambahan panjang pegas pada susunan seri sama dengan pertambahan
panjang pegas tunggal adalah.
15. Perhatikan gambar sususan
pegas disamping:
Jika k1=30 N/m, k2=4k1 N/m, k3=3k1 N/m, k4=1,5k3
N/m, k5=2k2 N/m dan F=200 N. Tentukan pertambahan panjang susunan pegas
tersebut.
16. Hitunglah energi potensial elastis sebuah pegas yang ditarik oleh
suatu gaya 80 N. Jika tetapan pegas 200 N/m.
17. Pertambahan
panjang sebuah pegas yang ditarik oleh gaya sebesar 5 N sebesar 30 cm.
Energi potensial elastis pegasnya sebesar..... Joule
18. Diketahui Panjang= 5 cm ditarik gaya = 10 N Ditanya A.pertambahan
panjang pegas bila ditarik gaya sebesar 15 N B. Besar energi potensial
elastis pegas saat ditarik gaya sebesar 15 N
19.
Energi potensial pegas ketika di tarik sehingga memendek sepanjang 5
cm adalah 500 Joule. Pegas harus ditekan berapa cm lagi supaya energi
potensial menjadi 2500 joule
20.
Perhatikan grafik hubungan gaya ΔF dengan pertambahan panjang Δx pada
suatu pegas di bawah! Berdasarkan grafik, maka pegas bersifat plastis pada
gaya tarik sebesar
A. 0 sampai 4 N
B. 0 sampai 8 N
C. 0 sampai 12 N
D. 8
N sampai 12 N
E. 8 N sampai 16 N
Semoga dengan contoh-contoh soal ini semakin mengasah kemampuan teman-teman dalam menjawab soal-soal Hukum Hooke baik dalam latihan, ulangan ataupun ujian.
Bila ada yang keliru dan ingin ditanyakan silahkan tinggalkan komentar.
Selamat belajar!
Terinspirasi oleh, brainly.co.id dan gurumuda.net.☺












Post a Comment for "Kumpulan Contoh Soal dan Pembahasan Hukum Hooke dan Elastisitas serta Rumusnya. Lengkap"