10+ Contoh Latihan Soal dan Pembahasan/Penyelesaian Ulangan Materi Gerak Parabola

Assalammualaikum wr.wb teman-teman, pada artikel kali ini masharist.com akan membahas tentang Contoh Latihan Soal dan Pembahasan/Penyelesaian Ulangan Gerak Parabola

Gerak Parabola merupakan materi fisika yang diajarkan kepada kelas x SMA.Materi ini berkaitan erat dengan sudut dan juga gerak suatu benda

Semoga artikel ini bermanfaat bagi semuanya.

Pada contoh soal ulangan Gerak Parabola ini, pada pilihan ganda akan tersedia pembahasan. Namun dalam essay hanya berupa soal. Agar teman-teman dapat menjadikannya sebagai latihan. Tetap semangat. Tetap menjadi anak yang rajin. Selamat membaca. Doakan kami agar terus bermanfaat ya. Amin

10+ Contoh Latihan Soal dan Pembahasan/Penyelesaian Ulangan Materi Gerak Parabola

 

ULANGAN HARIAN

BAB Gerak Parabola

NAMA       :

KELAS      :

A. PILIHAN GANDA

1.

Diketahui sebuah peluru ditembakkan dengan kecepatan 40 m/s jika sudut elevasinya 60° dan percepatan gravitasi = 10 m/s² maka peluru mencapai titik tertinggi setelah
a. 2√3 sekon
b. √3 sekon
c. 1 sekon
d. 2 sekon
e. 3 sekon

Penyelesaian dan Pembahasan Soal

Diketahui :

kecepatan awal diam (vo) = 40 m/s
sudut elevasinya (α) = 60°
gravitasi (g)=10 m/s²

Ditanya :
waktu saat dititik tertinggi (tm) ?

Jawaban:

Mencari ketinggian maksimum

Hm = vo²sin²α/2g
   = 40².sin²60/ 2.10
   = 1600.(¹/₂√3)²/20
   = 60 meter

waktu saat dititik tertinggi
tm = √(2Hm)/(g)
tm = √(2.60)/(10)
tm = √(120)/(10)
tm = √(12) = 2√3 sekon (a)

Jadi, waktu saat dititik tertinggi  adalah 2√3 sekon (a)

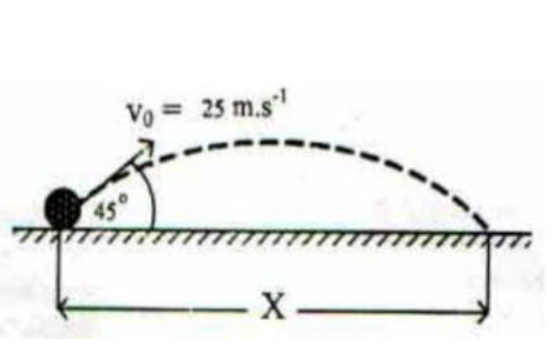
2. Apabila seorang Atlet sepak bola menendang bola dengan lintasan seperti pada gambar. Jarak x adalah.... (g=10 m/s²) V0 = 25 m/s, α=45°
a. 52,5 meter
b. 62,5 meter
c. 72,5 meter
d. 82,5 meter
e. 92,5 meter

Penyelesaian dan Pembahasan Soal

Diketahui :

kecepatan awal diam (vo) = 25 m/s
sudut elevasinya (α) = 45°
gravitasi (g)=10 m/s²

Ditanya :
Jarak x ?

Jawaban:

Mencari lama bola di udara

tx maks = (2.vo.sin(α))/g
tx maks = (2.25.sin(45))/10
tx maks = (50.0,5√2)/10
tx maks = (25√2)/10 = 2,5√2 sekon

Mencari jarak terjauh

x maks = (vo².sin(2α))/g
x maks = (25².sin(2.45))/10
x maks = (625. 1))/10 = 62,5 meter

Jadi, jarak terjauh  adalah  62,5 meter (b)
 

3. Sebuah peluru ditembakkan dengan lintasan. Lintasan dapat dilihat pada gambar dibawah apabila gravitasi adalah 10 m/s². Tinggi maksimum yang dicapai peluru adalah
a. 5 meter
b. 6 meter
c. 7 meter
d. 8 meter
e. 9 meter 

Penyelesaian dan Pembahasan Soal

Diketahui :

kecepatan awal diam (vo) = 20 m/s
sudut elevasinya (α) = 30°
gravitasi (g)=10 m/s²

Ditanya :
Tinggi maksimum?

Jawaban:

Mencari ketinggian maksimum

Hm = vo²sin²α/2g
   = 20².sin²30/ 2.10
   = 400.(¹/₂)²/20
   = 5 meter

Tinggi maksimum yang dicapai peluru adalah 5 meter.(a)

4. Apabila seseorang memegang bola pada ketinggian 20 meter lalu melempar horisontal ke depan dengan kecepatan awal 5 m/s. Tentukan selang waktu bola tiba di tanah...
a. 5 meter
b. 6 meter
c. 7 meter
d. 8 meter
e. 9 meter

Penyelesaian dan Pembahasan Soal

Diketahui :

tinggi (h) = 20 Meter
kecepatan awal diam (vo) = 5 m/s
gravitasi (g)=10 m/s²

Ditanya :
Selang waktu bola tiba di tanah

Jawaban:

t = √(2h)/(g)
t = √(2(20)/(10)
t = √4 = 2 sekon

Selang waktu bola tiba di tanah adalah 2 sekon.

5.

Apabila diketahui sebuah peluru ditembakkan dengan kecepatan 20 m/s jika sudut elevasinya 60° dan percepatan gravitasi = 10 m/s² maka peluru mencapai titik tertinggi setelah
a. 2√3 sekon
b. √3 sekon
c. 1 sekon
d. 2 sekon
e. 3 sekon

Penyelesaian dan Pembahasan Soal

Diketahui :

kecepatan awal diam (vo) = 20 m/s
sudut elevasinya (α) = 60°
gravitasi (g)=10 m/s²

Ditanya :
waktu saat dititik tertinggi (tm) ?

Jawaban:

Mencari ketinggian maksimum

Hm = vo²sin²α/2g
   = 20².sin²60/ 2.10
   = 400.(¹/₂√3)²/20
   = 15 meter

waktu saat dititik tertinggi
tm = √(2Hm)/(g)
tm = √(2.15)/(10)
tm = √(30)/(10)
tm = √(3) = √3 sekon (b)

Jadi, waktu saat dititik tertinggi  adalah √3 sekon (b)

6.  

 Diketahui sebuah peluru ditembakkan dengan kecepatan tertentu. Jika sudut elevasinya 60° dan percepatan gravitasi = 10 m/s². Tentukanlah kecepatan peluru, jika peluru mencapai titik tertinggi setelah √3 sekon
a. 20 m/s
b. 30 m/s
c. 1 m/s
d. 2 m/s
e. 3 m/s

Penyelesaian dan Pembahasan Soal

Diketahui :
waktu saat dititik tertinggi (tm) = √3 sekon
sudut elevasinya (α) = 60°
gravitasi (g)=10 m/s²

Ditanya :
kecepatan awal (vo) =  ?

Jawaban:

Mencari ketinggian maksimum

tm = √(2Hm)/(g)
√3 = √(2.Hm)/(10)
√3 = √(2Hm)/(10)
√3 = √(Hm/5)
Hm/5 = 3
Hm = 3.5 = 15 meter

Mencari Kecepatan awal

Hm = vo²sin²α/2g
15 = vo².sin²60/ 2.10
15  = vo².(¹/₂√3)²/20
300 = 3/4 . vo²
1200 = 3 . vo²
vo² = 1200/3 =400
vo = 20 m/s

Jadi, kecepatan awal adalah  20 m/s (a)

 

7. Apabila sebuah peluru ditembakkan dengan kecepatan tertentu yaitu 20 m/s. Jika peluru mencapai titik tertinggi setelah √3 sekon dan dan percepatan gravitasi = 10 m/s² tentukan sudut elevasinya.
a. 60°
b. 30°
c. 20°
d. 10°
e. 0°

Penyelesaian dan Pembahasan Soal

Diketahui :
waktu saat dititik tertinggi (tm) = √3 sekon
kecepatan awal (vo) = 20 m/s
gravitasi (g)=10 m/s²

Ditanya :
sudut elevasinya (α) =  ?

Jawaban:

Mencari ketinggian maksimum

tm = √(2Hm)/(g)
√3 = √(2.Hm)/(10)
√3 = √(2Hm)/(10)
√3 = √(Hm/5)
Hm/5 = 3
Hm = 3.5 = 15 meter

Mencari Sudut elevasi

Hm = vo²sin²α/2g
15 = 20².sin²α/ 2.10
15  = 400.(sin α)²/20
300 = 400.(sin α)²
300/400 = (sin α)²
√(3/4) = sin α
¹/₂√3 = sin α
α = 60°

Jadi, sudut elevasinya (α) adalah 60° (a)

8. Apabila seorang Atlet sepak bola menendang bola dengan lintasan seperti pada gambar. Bila jarak terjauh atau x adalah 62,5 meter dan gravitasi adalah 10 m/s² serta sudut elevasi 45°, tentukan kecepatan awal dari bola tersebut...
a. 0,5 m/s
b. 25 m/s
c. 30 m/s
d. 45 m/s
e. 50 m/s

Penyelesaian dan Pembahasan Soal

Diketahui :
Jarak terjauh (x) = 62,5 meter
sudut elevasinya (α) = 45°
gravitasi (g)=10 m/s²

Ditanya :
kecepatan awal (vo) =?

Jawaban:

Mencari kecepatan awal

x maks = (vo².sin(2α))/g
62,5 = (vo².sin(2.45))/10
62,5 = (vo². 1))/10
625 = (vo². 1)
vo = √625 = 25 m/s

Jadi, kecepatan awal (vo) adalah 25 m/s (b)

 

 9. Diketahui apabila seorang Atlet sepak bola menendang bola dengan lintasan seperti pada gambar. Jarak x adalah 62,5 meter (g=10 m/s²) vo = 25 m/s, Tentukan nilai sudut elevasinya (α)?
a. 35°
b. 45°
c. 55°
d. 65°
e. 75°

Penyelesaian dan Pembahasan Soal

Diketahui :
Jarak x = 62,5 meter
kecepatan awal diam (vo) = 25 m/s
gravitasi (g)=10 m/s²

Ditanya :
sudut elevasinya (α) = ?

Jawaban:

Mencari sudut elevasinya (α)

x maks = (vo².sin(2α))/g
62,5 = (25².sin(2.α))/10
62,5 = (625.sin(2.α))/10
625  = 625 . sin(2.α)
1 = sin(2.α)
2.α = 90°
α = 45°

Jadi, sudut elevasinya (α) adalah 45° (b)

10. Apabila diketahui sebuah peluru ditembakkan dengan lintasan. Lintasan dapat dilihat pada gambar dibawah, apabila gravitasi adalah 10 m/s². Serta tinggi maksimum yang dicapai peluru adalah 5 meter. Tentukan kecepatan awal peluru....
a. 20 m/s
b. 25 m/s
c. 30 m/s
d. 45 m/s
e. 50 m/s 

Penyelesaian dan Pembahasan Soal

Diketahui :
Tinggi maksimum (Hm) = 5 meter.
sudut elevasinya (α) = 30°
gravitasi (g)=10 m/s²

Ditanya :
kecepatan awal diam (vo) = ?

Jawaban:

Mencari Kecepatan awal (vo)

Hm = vo²sin²α/2g
5  = vo².sin²30/ 2.10
5  = vo².(¹/₂)²/20
100= vo²/4
vo²=400
vo =20 m/s

Maka kecepatan awal peluru adalah 20 m/s(a)

11. Terdapat sebuah peluru ditembakkan dengan lintasan. Lintasan dapat dilihat pada gambar dibawah, apabila gravitasi adalah 10 m/s². Serta tinggi maksimum yang dicapai peluru adalah 5 meter dan kecepatan awal peluru ditembakkan adalah 20 m/s, maka tentukanlah sudut elevasinya....
a. 30°
b. 45°
c. 55°
d. 65°
e. 75°

Penyelesaian dan Pembahasan Soal

Diketahui :
Tinggi maksimum (Hm) = 5 meter.
kecepatan awal diam (vo) = 20 m/s
gravitasi (g)=10 m/s²

Ditanya :
sudut elevasinya (α) = ..°?

Jawaban:

Mencari Sudut elevasinya

Hm = vo²sin²α/2g
5  = 20².sin²α/ 2.10
5  = 400.(sinα)²/20
100= 400.(sinα)²
100/400=(sinα)²
1/4=(sinα)²
sinα=√(1/4) =1/2
α=30°

Maka sudut elevasinya (α) adalah 30° (a)

 

B. Essay

1. Diketahui sebuah bola meriam ditembakkan dengan kecepatan 80 m/s jika sudut elevasinya 30° dan percepatan gravitasi = 10 m/s² maka bola meriam mencapai titik tertinggi setelah

 

2.  Dari soal no. 1 essay, tentukan perbandingan titik tertinggi jika kecepatan awal dikurangi sebanyak 25%

 

3. Perhatikan Gambar dibawah. Tentukan nilai X apabila :

a. Nilai Vo sama dengan gambar

b. Nilai Vo dinaikkan 25%

c. Nilai Vo dikurangi 25 %

 

 

Semoga dengan contoh-contoh soal ini semakin mengasah kemampuan teman-teman dalam menjawab Ulangan Materi Gerak Parabola. Semoga bermanfaat.

Berikut kata kunci terkait Ulangan Materi Gerak Parabola yang bisa teman-teman cari di google, semoga bermanfaat 

Searches related to Ulangan 4 - Gerak Parabola
soal gerak parabola dan pembahasannya
rumus gerak parabola
contoh soal gerak parabola sbmptn
contoh soal gerak parabola brainly
soal gerak parabola pdf
contoh gerak parabola
mencari kecepatan awal gerak parabola
soal gerak parabola fisika study center
contoh soal gerak parabola sbmptn
contoh soal gerak parabola brainly
soal gerak parabola pdf
rumus gerak parabola
mencari kecepatan awal gerak parabola
soal gerak parabola pilihan ganda
soal gerak parabola fisika study center
contoh gerak parabola
rumus gerak parabola brainly
pembuktian rumus gerak parabola
rumus ketinggian maksimum gerak parabola
gerak parabola dalam kehidupan sehari hari
soal gerak parabola
contoh gerak parabola
pengertian gerak parabola
gerak parabola pdf
rumus gerak parabola
soal gerak parabola pdf
contoh gerak parabola dalam kehidupan sehari hari
materi gerak parabola pdf
materi gerak parabola kelas 10
rumus gerak parabola
contoh gerak parabola
gerak parabola ppt
pengertian gerak parabola
dasar teori gerak parabola
laporan gerak parabola
contoh gerak parabola dalam kehidupan sehari hari
contoh gerak parabola brainly
rumus gerak parabola
contoh soal gerak parabola
pengertian gerak parabola
contoh gerak parabola adalah brainly
contoh gerak melingkar
manfaat gerak parabola
rumus ketinggian maksimum gerak parabola
gerak parabola dalam kehidupan sehari hari
contoh soal gerak parabola dan pembahasannya
gerak parabola pdf
rumus gerak parabola brainly
rumus ketinggian maksimum gerak vertikal ke atas
apa saja yang mempengaruhi kecepatan pada gerak parabola? jelaskan!
ciri ciri gerak parabola
Contoh soal gerak parabola sbmptn
rumus gerak parabola
gerak melingkar fisika study center
soal gerak parabola pdf
contoh soal gerak parabola brainly
rumus jarak mendatar
mencari kecepatan awal gerak parabola
dua anak panah a dan b ditembakkan
soal gerak parabola dan pembahasannya
rumus gerak parabola
contoh soal gerak parabola sbmptn
contoh soal gerak parabola brainly
soal gerak parabola pdf
contoh gerak parabola
mencari kecepatan awal gerak parabola
soal gerak parabola fisika study center

 

Share :