Kumpulan Contoh Soal dan Pembahasan Gerak Parabola serta Rumusnya. Lengkap

Assalammualaikum teman-teman, pada artikel kali ini masharist.com akan membahas tentang Contoh Latihan Soal Gerak Parabola dan Pembahasannya. Bagi yang ingin soal latihan dapat klik disini, Semoga bermanfaat

Daftar Isi

• Deskripsi Singkat
• Definisi
• Rumus Gerak Parbola
• Kumpulan Contoh Soal Gerak Parabola
• Contoh Soal Gerak Parabola : Menghitung tan α
• Contoh Soal Gerak Parabola : Menghitung sudut elevasi (α)
• Contoh Soal Gerak Parabola : Menghitung Kecepatan Awal (Vo)
• Contoh Soal Gerak Parabola : Menghitung sudut Tinggi Maksimum
• Contoh Soal dan Pembahasan Gerak Parabola
  
• Bagi yang ingin soal latihan dapat klik disini,
  
  

Deskripsi Singkat

Apa itu Gerak Parbola? Gerak yang lintasannya berbentuk parabola disebut gerak parabola. Dalam fisika, suatu benda yang dilemparkan dan membentuk sudut dengan bidang horizontal akan membentuk lintasan parabola.

Definisi
Pengertian gerak parabola adalah perpaduan gerak lurus dengan kecepatan konstan dan percepatan konstan. Sesuai namanya, lintasan gerak ini berupa lintasan parabola.

Gerak Parabola juga dikenal sebagai Gerak Peluru. Dinamakan Gerak parabola karena lintasannya berbentuk parabola, bukan bergerak lurus. Contoh bentuk gerak ini dapat kita lihat pada gerakan bola saat dilempar, gerakan pada peluru meriam yang ditembakkan, gerakan pada benda yang dilemparkan dari pesawat dan gerakan pada seseorang yang melompat maju.

Rumus Gerak Parbola

Kumpulan Contoh Soal dan Pembahasan Gerak Parabola

Contoh Soal Gerak Parabola : Menghitung tan α

Soal nomor 1

1. Sebuah peluru ditembakkan sedemikian rupa sehingga jarak tembakannya sama dengan tiga kali tinggi maksimum. Jika sudut elevasi α , maka besar tan α adalah

Pembahasan

Diketahui :

Jarak tembakan (Xmax) = 3 kali tinggi maksimum (H max)

Ditanya :

tan α =?

Jawaban:

Soal nomor 2

2. Diketahui terdapat sebuah peluru ditembakkan sedemikian rupa sehingga jarak tembakannya sama dengan empat kali tinggi maksimum. Jika diketahui sudut elevasi α , maka besar dari tan α adalah

Pembahasan

Diketahui :

Jarak tembakan (Xmax) = 4 kali tinggi maksimum (H max)

Ditanya :

tan α =?

Jawaban:

Contoh Soal Gerak Parabola : Menghitung sudut elevasi (α)

Soal nomor 1

1. Sebuah peluru ditembakkan ke atas dengan kecepatan awal sebesar 20 m/s dan mengenai sandaran yang memiliki jarak mendatar sejauh 40 m. Apabila percepatan gravitasinya adalah sebesar 10 m/s2. Tentukanlah sudut elevasi pada gerak peluru tersebut.

Pembahasan

Diketahui :

Kecepatan awal (Vo) = 20 m/s
Jarak mendatar (Xmax) = 40 m
Gravitasi (g) = 10 m/s2

Ditanya :

Sudut elevasi (α) =?

Jawaban

Contoh Soal Gerak Parabola : Menghitung Kecepatan Awal (Vo)

Soal nomor 1

1. Sebuah benda dilempar dengan kecepatan awal. VO dan sudut elevasi 60 derajat. Ketika benda mencapai tinggi maksimum,jarak mendatar yang di tempuhnya 10√3 m.kecepatan awal tersebut adalah…Ms-1

Pembahasan

Diketahui :
Sudut elevasi (α) = 60 derajat
Saat Ymax, X = 10√3 m
Gravitasi (g) = 10 m/s2

Ditanya :

kecepatan awal(vo) =?

Jawaban

Ketika benda mencapai ketinggian maksimum, jarak tempuh horizontal sama dengan setengah jangkauan maksimumnya. Sehingga,

Contoh Soal Gerak Parabola : Menghitung Tinggi Maksimum

1. Peluru A dan B ditembakkan dari senapan yang sama dg sudut elevasi yg berbeda, peluru A dg sudut 30derajat. Dan peluru B dg sudut 60 derajat berapakah perbandingan antara tinggi max yg dicapai peluru A dan peluru B?
Pembahasan

Diketahui :
Sudut elevasi (αA) = 30 derajat
Sudut elevasi (αB) = 60 derajat

Ditanya :

Perbandingan antara tinggi max dicapai peluru A dan B =?

Jawaban

Contoh Soal dan Pembahasan Gerak Parabola

1.
Diketahui sebuah peluru ditembakkan dengan kecepatan 40 m/s jika sudut elevasinya 60° dan percepatan gravitasi = 10 m/s² maka peluru mencapai titik tertinggi setelah
a. 2√3 sekon
b. √3 sekon
c. 1 sekon
d. 2 sekon
e. 3 sekon

Penyelesaian dan Pembahasan Soal

Diketahui :

kecepatan awal diam (vo) = 40 m/s
sudut elevasinya (α) = 60°
gravitasi (g)=10 m/s²

Ditanya :
waktu saat dititik tertinggi (tm) ?

Jawaban:

Mencari ketinggian maksimum

Hm = vo²sin²α/2g
   = 40².sin²60/ 2.10
   = 1600.(¹/₂√3)²/20
   = 60 meter

waktu saat dititik tertinggi
tm = √(2Hm)/(g)
tm = √(2.60)/(10)
tm = √(120)/(10)
tm = √(12) = 2√3 sekon (a)

Jadi, waktu saat dititik tertinggi  adalah 2√3 sekon (a)

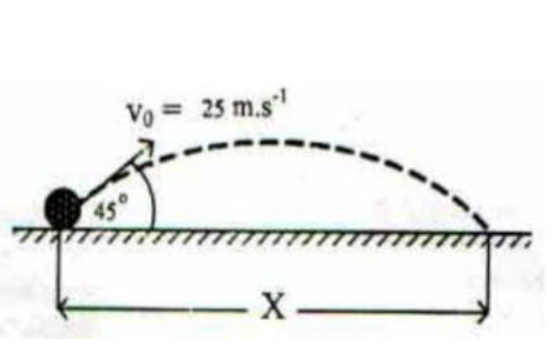
2. Apabila seorang Atlet sepak bola menendang bola dengan lintasan seperti pada gambar. Jarak x adalah.... (g=10 m/s²) V0 = 25 m/s, α=45°
a. 52,5 meter
b. 62,5 meter
c. 72,5 meter
d. 82,5 meter
e. 92,5 meter

Penyelesaian dan Pembahasan Soal

Diketahui :

kecepatan awal diam (vo) = 25 m/s
sudut elevasinya (α) = 45°
gravitasi (g)=10 m/s²

Ditanya :
Jarak x ?

Jawaban:

Mencari lama bola di udara

tx maks = (2.vo.sin(α))/g
tx maks = (2.25.sin(45))/10
tx maks = (50.0,5√2)/10
tx maks = (25√2)/10 = 2,5√2 sekon

Mencari jarak terjauh

x maks = (vo².sin(2α))/g
x maks = (25².sin(2.45))/10
x maks = (625. 1))/10 = 62,5 meter

Jadi, jarak terjauh  adalah  62,5 meter (b)
 

3. Sebuah peluru ditembakkan dengan lintasan. Lintasan dapat dilihat pada gambar dibawah apabila gravitasi adalah 10 m/s². Tinggi maksimum yang dicapai peluru adalah
a. 5 meter
b. 6 meter
c. 7 meter
d. 8 meter
e. 9 meter 

Penyelesaian dan Pembahasan Soal

Diketahui :

kecepatan awal diam (vo) = 20 m/s
sudut elevasinya (α) = 30°
gravitasi (g)=10 m/s²

Ditanya :
Tinggi maksimum?

Jawaban:

Mencari ketinggian maksimum

Hm = vo²sin²α/2g
   = 20².sin²30/ 2.10
   = 400.(¹/₂)²/20
   = 5 meter

Tinggi maksimum yang dicapai peluru adalah 5 meter.(a)

4. Apabila seseorang memegang bola pada ketinggian 20 meter lalu melempar horisontal ke depan dengan kecepatan awal 5 m/s. Tentukan selang waktu bola tiba di tanah...
a. 5 meter
b. 6 meter
c. 7 meter
d. 8 meter
e. 9 meter

Penyelesaian dan Pembahasan Soal

Diketahui :

tinggi (h) = 20 Meter
kecepatan awal diam (vo) = 5 m/s
gravitasi (g)=10 m/s²

Ditanya :
Selang waktu bola tiba di tanah

Jawaban:

t = √(2h)/(g)
t = √(2(20)/(10)
t = √4 = 2 sekon

Selang waktu bola tiba di tanah adalah 2 sekon.

5.

Apabila diketahui sebuah peluru ditembakkan dengan kecepatan 20 m/s jika sudut elevasinya 60° dan percepatan gravitasi = 10 m/s² maka peluru mencapai titik tertinggi setelah
a. 2√3 sekon
b. √3 sekon
c. 1 sekon
d. 2 sekon
e. 3 sekon

Penyelesaian dan Pembahasan Soal

Diketahui :

kecepatan awal diam (vo) = 20 m/s
sudut elevasinya (α) = 60°
gravitasi (g)=10 m/s²

Ditanya :
waktu saat dititik tertinggi (tm) ?

Jawaban:

Mencari ketinggian maksimum

Hm = vo²sin²α/2g
   = 20².sin²60/ 2.10
   = 400.(¹/₂√3)²/20
   = 15 meter

waktu saat dititik tertinggi
tm = √(2Hm)/(g)
tm = √(2.15)/(10)
tm = √(30)/(10)
tm = √(3) = √3 sekon (b)

Jadi, waktu saat dititik tertinggi  adalah √3 sekon (b)

6.  

 Diketahui sebuah peluru ditembakkan dengan kecepatan tertentu. Jika sudut elevasinya 60° dan percepatan gravitasi = 10 m/s². Tentukanlah kecepatan peluru, jika peluru mencapai titik tertinggi setelah √3 sekon
a. 20 m/s
b. 30 m/s
c. 1 m/s
d. 2 m/s
e. 3 m/s

Penyelesaian dan Pembahasan Soal

Diketahui :
waktu saat dititik tertinggi (tm) = √3 sekon
sudut elevasinya (α) = 60°
gravitasi (g)=10 m/s²

Ditanya :
kecepatan awal (vo) =  ?

Jawaban:

Mencari ketinggian maksimum

tm = √(2Hm)/(g)
√3 = √(2.Hm)/(10)
√3 = √(2Hm)/(10)
√3 = √(Hm/5)
Hm/5 = 3
Hm = 3.5 = 15 meter

Mencari Kecepatan awal

Hm = vo²sin²α/2g
15 = vo².sin²60/ 2.10
15  = vo².(¹/₂√3)²/20
300 = 3/4 . vo²
1200 = 3 . vo²
vo² = 1200/3 =400
vo = 20 m/s

Jadi, kecepatan awal adalah  20 m/s (a)

 

7. Apabila sebuah peluru ditembakkan dengan kecepatan tertentu yaitu 20 m/s. Jika peluru mencapai titik tertinggi setelah √3 sekon dan dan percepatan gravitasi = 10 m/s² tentukan sudut elevasinya.
a. 60°
b. 30°
c. 20°
d. 10°
e. 0°

Penyelesaian dan Pembahasan Soal

Diketahui :
waktu saat dititik tertinggi (tm) = √3 sekon
kecepatan awal (vo) = 20 m/s
gravitasi (g)=10 m/s²

Ditanya :
sudut elevasinya (α) =  ?

Jawaban:

Mencari ketinggian maksimum

tm = √(2Hm)/(g)
√3 = √(2.Hm)/(10)
√3 = √(2Hm)/(10)
√3 = √(Hm/5)
Hm/5 = 3
Hm = 3.5 = 15 meter

Mencari Sudut elevasi

Hm = vo²sin²α/2g
15 = 20².sin²α/ 2.10
15  = 400.(sin α)²/20
300 = 400.(sin α)²
300/400 = (sin α)²
√(3/4) = sin α
¹/₂√3 = sin α
α = 60°

Jadi, sudut elevasinya (α) adalah 60° (a)

8. Apabila seorang Atlet sepak bola menendang bola dengan lintasan seperti pada gambar. Bila jarak terjauh atau x adalah 62,5 meter dan gravitasi adalah 10 m/s² serta sudut elevasi 45°, tentukan kecepatan awal dari bola tersebut...
a. 0,5 m/s
b. 25 m/s
c. 30 m/s
d. 45 m/s
e. 50 m/s

Penyelesaian dan Pembahasan Soal

Diketahui :
Jarak terjauh (x) = 62,5 meter
sudut elevasinya (α) = 45°
gravitasi (g)=10 m/s²

Ditanya :
kecepatan awal (vo) =?

Jawaban:

Mencari kecepatan awal

x maks = (vo².sin(2α))/g
62,5 = (vo².sin(2.45))/10
62,5 = (vo². 1))/10
625 = (vo². 1)
vo = √625 = 25 m/s

Jadi, kecepatan awal (vo) adalah 25 m/s (b)

 

 9. Diketahui apabila seorang Atlet sepak bola menendang bola dengan lintasan seperti pada gambar. Jarak x adalah 62,5 meter (g=10 m/s²) vo = 25 m/s, Tentukan nilai sudut elevasinya (α)?
a. 35°
b. 45°
c. 55°
d. 65°
e. 75°

Penyelesaian dan Pembahasan Soal

Diketahui :
Jarak x = 62,5 meter
kecepatan awal diam (vo) = 25 m/s
gravitasi (g)=10 m/s²

Ditanya :
sudut elevasinya (α) = ?

Jawaban:

Mencari sudut elevasinya (α)

x maks = (vo².sin(2α))/g
62,5 = (25².sin(2.α))/10
62,5 = (625.sin(2.α))/10
625  = 625 . sin(2.α)
1 = sin(2.α)
2.α = 90°
α = 45°

Jadi, sudut elevasinya (α) adalah 45° (b)

10. Apabila diketahui sebuah peluru ditembakkan dengan lintasan. Lintasan dapat dilihat pada gambar dibawah, apabila gravitasi adalah 10 m/s². Serta tinggi maksimum yang dicapai peluru adalah 5 meter. Tentukan kecepatan awal peluru....
a. 20 m/s
b. 25 m/s
c. 30 m/s
d. 45 m/s
e. 50 m/s 

Penyelesaian dan Pembahasan Soal

Diketahui :
Tinggi maksimum (Hm) = 5 meter.
sudut elevasinya (α) = 30°
gravitasi (g)=10 m/s²

Ditanya :
kecepatan awal diam (vo) = ?

Jawaban:

Mencari Kecepatan awal (vo)

Hm = vo²sin²α/2g
5  = vo².sin²30/ 2.10
5  = vo².(¹/₂)²/20
100= vo²/4
vo²=400
vo =20 m/s

Maka kecepatan awal peluru adalah 20 m/s(a)

Semoga dengan contoh-contoh soal ini semakin mengasah kemampuan teman-teman dalam menjawab soal-soal Gerak Parabola baik dalam latihan, ulangan ataupun ujian.
Bagi yang ingin soal latihan dapat klik disini,

Bila ada yang keliru dan ingin ditanyakan silahkan tinggalkan komentar.

Selamat belajar!

Terinspirasi oleh :
https://brainly.co.id/tugas/13041309
https://brainly.co.id/tugas/2137418
https://brainly.co.id/tugas/428885
https://brainly.co.id/tugas/18536214
https://www.kompas.com/skola/read/2020/11/26/165618669/contoh-soal-gerak-parabola
https://www.kompas.com/skola/read/2020/12/31/192559569/gerak-parabola-menghitung-kecepatan-awal

Share :